Question

7．O为直线DA上一点，OB⊥OF，EO是∠AOB的平分线．

（1）如图（1），若∠AOB=130°，求∠EOF的度数；
（2）若∠AOB=α，90°＜α＜180°，求∠EOF的度数；
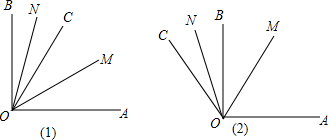
（3）若∠AOB=α，0°＜α＜90°，请在图（2）中画出射线OF，使得（2）中∠EOF的结果仍然成立．

Answer 1

分析 （1）首先利用角平分线的定义可得∠AOE的度数，由垂直的定义得∠BOF=90°，易得∠AOF，可得∠EOF；
（2）首先利用角平分线的定义可得∠AOE=$\frac{1}{2}α$，由垂直的定义得∠BOF=90°，易得∠AOF=α-90°，可得∠EOF；
（3）根据题意OB⊥OF，使得（2）中∠EOF的结果仍然成立，画出射线OF即可，再结合图形同理（2）可得结果．

解答 解：（1）∵∠AOB=130°，EO是∠AOB的平分线，
∴$∠AOE=\frac{1}{2}∠AOB=\frac{1}{2}×130°$=65°，
∵OB⊥OF，
∴∠BOF=90°，
∴∠AOF=∠AOB-∠BOF=130°-90°=40°，
∴∠EOF=∠AOE-∠AOF=65°-40°=25°；

（2）∵∠AOB=α，90°＜α＜180°，EO是∠AOB的平分线，
∴∠AOE=$\frac{1}{2}α$，
∵∠BOF=90°，
∴∠AOF=α-90°，
∴∠EOF=∠AOE-∠AOF=$\frac{1}{2}α$-（α-90°）=90$°-\frac{1}{2}α$；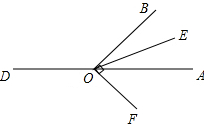

（3）如图，∵∠AOB=α，0°＜α＜90°，
∴∠BOE=∠AOE=$\frac{1}{2}α$，
∵∠BOF=90°，
∴∠EOF=∠BOF-∠BOE=90$°-\frac{1}{2}α$．

点评 本题主要考查了角平分线的定义和垂直的定义，结合图形利用角平分线的定义和垂直的定义是解答此题的关键．