题目内容
8.观察下列算式:①1×3-22=3-4=-1;
②2×4-32=8-9=-1
③3×5-42=15-16=-1
…
(1)请你按以上规律写出第4个算式;
(2)把这个规律用含字母n的式子表示出来,并用学过的整式乘法的有关知识,说明其成立的理由.
分析 (1)根据①②③的算式中,变与不变的部分,找出规律,写出新的算式;
(2)将(1)中,发现的规律,由特殊到一般,得出结论;进一步利用整式的混合运算方法加以证明.
解答 解:(1)第4个算式为:4×6-52=24-25=-1;
(2)用含字母n的式子表示出来为n(n+2)-(n+1)2=-1;
理由:n(n+2)-(n+1)2=n2+2n-(n2+2n+1)
=n2+2n-n2-2n-1=-1.
故n(n+2)-(n+1)2=-1成立.
点评 此题考查数字的变化规律,关键是由特殊到一般,得出一般规律,运用整式的运算进行检验.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
3.若一元一次不等式组$\left\{\begin{array}{l}{x≤7}\\{x-1≥m}\end{array}\right.$有解,则m的取值范围是( )
| A. | m>6 | B. | m≥6 | C. | m<7 | D. | m≤6 |
13.估计$\sqrt{8}$×$\sqrt{\frac{1}{2}}$+$\sqrt{18}$的运算结果应在哪两个连续自然数之间( )
| A. | 5和6 | B. | 6和7 | C. | 7和8 | D. | 8和9 |
 将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.求证:△CDO是等腰三角形.
将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.求证:△CDO是等腰三角形.
 如图所示,直径为10的圆A经过点C(0,5)和点O (0,0),B是y轴右侧圆A优弧上一点,那么sin∠OBC的值是$\frac{1}{2}$.
如图所示,直径为10的圆A经过点C(0,5)和点O (0,0),B是y轴右侧圆A优弧上一点,那么sin∠OBC的值是$\frac{1}{2}$.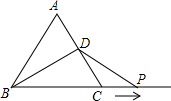 如图,等边三角形ABC的边长为10厘米.点D是边AC的中点.动点P从点C出发,沿BC的延长线以2厘米/秒的速度作匀速运动,设点P的运动时间为t(秒).若△BDP是等腰三角形,则为t=2.5.
如图,等边三角形ABC的边长为10厘米.点D是边AC的中点.动点P从点C出发,沿BC的延长线以2厘米/秒的速度作匀速运动,设点P的运动时间为t(秒).若△BDP是等腰三角形,则为t=2.5.