题目内容
20. 如图所示,直径为10的圆A经过点C(0,5)和点O (0,0),B是y轴右侧圆A优弧上一点,那么sin∠OBC的值是$\frac{1}{2}$.
如图所示,直径为10的圆A经过点C(0,5)和点O (0,0),B是y轴右侧圆A优弧上一点,那么sin∠OBC的值是$\frac{1}{2}$.
分析 作直径OE,连接CE,则OE=10,根据圆周角定理得出∠E=∠B,解直角三角形求出sinE即可.
解答 解:如图: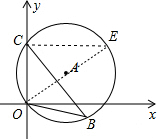
作直径OE,连接CE,
则OE=10,
根据圆周角定理得:∠E=∠B,
∵OE为直径,
∴∠OCE=90°,
∵C(0,5),
∴OC=5,
∴sin∠OBC=sinE=$\frac{OC}{OE}$=$\frac{5}{10}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了解直角三角形,圆周角定理的应用,能正确作出辅助线是解此题的关键,注意:在同圆或等圆中,圆周角等于它所夹弧所对的圆心角的一半.

练习册系列答案
相关题目
11.已知a,b为实数,则下列结论正确的是( )
| A. | 若a>b,则a-c<b-c | B. | 若a>b,则-a+c>-b+c | ||
| C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |
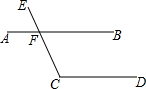 如图,AB∥CD,CE交AB于点F.若∠AFE=48°,则∠ECD=132°.
如图,AB∥CD,CE交AB于点F.若∠AFE=48°,则∠ECD=132°.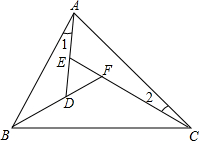 已知∠1=∠2,∠BAC=70°,求∠DEF的度数.
已知∠1=∠2,∠BAC=70°,求∠DEF的度数.