题目内容
18.关于x,y的二元一次方程y=kx+b(k,b为常数),当x=-1时,y=1;当x=1时,y=5.(1)求k,b的值;
(2)请直接写出这个方程的一组解(与已知的两组解不同).
分析 (1)把x与y的两对值代入方程求出k与b的值即可;
(2)由k与b的值确定出方程,找出与已知解不同的解即可.
解答 解:(1)把x=-1,y=1;x=1,y=5代入方程得:$\left\{\begin{array}{l}{-k+b=1}\\{k+b=5}\end{array}\right.$,
解得:k=2,b=3;
(2)把k=2,b=3代入方程得:y=2x+3,
令x=0,得到y=3,
则这个方程的一组解为x=0,y=3.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
8.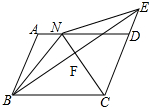 如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )
如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )
 如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )
如图,在?ABCD中,∠BCD的平分线CN交?ABCD的边AD于点N,BF⊥CN,交CN于点F,交CD的延长线交于点E,连接BN,NE.若BN=6,BC=8,则△DNE的周长为( )| A. | 14 | B. | 11 | C. | 9 | D. | 12 |
6.若实数$\sqrt{7}$,$\frac{2}{3}$,0,$\frac{22}{33}$,-0.628,$\sqrt{36}$,3.020 020 002…(每相邻两个2之间0的个数逐渐多1)中,属于正无理数的共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
3.下列说法正确的是( )
| A. | 平面内,过一点能作已知直线的一条平行线 | |
| B. | 平面内,过一点能作已知直线的一条垂线 | |
| C. | 射线AB的端点是A和B | |
| D. | 边长相等的多边形是正多边形 |
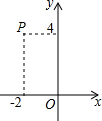 点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,则a的值是2或6.
点P在平面直角坐标系的位置如图所示,将点P向下平移a个单位得点P′,若点P′到x轴和y轴的距离均相等,则a的值是2或6.