题目内容
19. 将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.求证:△CDO是等腰三角形.
将一副直角三角板如图摆放,等腰直角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.求证:△CDO是等腰三角形.
分析 根据BC=DE和∠DEF=30°可求得∠BDC和∠BCD的值,根据∠ACB=45°即可求得∠DOC的值,即可解题.
解答 证明:∵在△BDC 中,BC=DB,
∴∠BDC=∠BCD.
∵∠DBE=30°,
∴∠BDC=∠BCD=75°,
∵∠ACB=45°,
∴∠DOC=30°+45°=75°.
∴∠DOC=∠BDC,
∴△CDO是等腰三角形.
点评 本题考查了等腰三角形的判定,等腰直角三角形的性质,本题中求证∠DOC=∠BDC是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.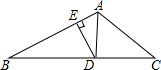 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )
 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )
如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=28,DE=4,AC=6,则AB的长是( )| A. | 8 | B. | 10 | C. | 12 | D. | 不能确定 |
11.已知a,b为实数,则下列结论正确的是( )
| A. | 若a>b,则a-c<b-c | B. | 若a>b,则-a+c>-b+c | ||
| C. | 若a>b,则ac2>bc2 | D. | 若ac2>bc2,则a>b |