题目内容
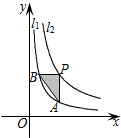 如图,函数y=
如图,函数y=| 1 |
| x |
| 3 |
| x |
考点:反比例函数系数k的几何意义
专题:
分析:将点P(m,n)代入反比例函数y=
(x>0)用m表示出n即可表示出点P的坐标,然后根据PB∥x轴,得到B点的纵坐标为
,然后将点B的纵坐标带人反比例函数的解析式y=
(x>0)即可得到点B的坐标,同理得到点A的坐标;根据PB=m-
=
,PA=
-
=
,利用S△PAB=
PA•PB即可得到答案;
| 3 |
| x |
| 3 |
| m |
| 1 |
| x |
| m |
| 3 |
| 2m |
| 3 |
| 3 |
| m |
| 1 |
| m |
| 2 |
| m |
| 1 |
| 2 |
解答:解:设点P(m,n),
∵P是反比例函数y=
(x>0)图象上的点,
∴n=
,
∴点P(m,
);
∵PB∥x轴,
∴B点的纵坐标为
,
将点B的纵坐标代入反比例函数的解析式y=
(x>0)得:x=
,
∴B(
,
),同理可得:A(m,
);
∵PB=m-
=
,PA=
-
=
,
∴S△PAB=
PA•PB=
×
×
=
.
故答案为
.
∵P是反比例函数y=
| 3 |
| x |
∴n=
| 3 |
| m |
∴点P(m,
| 3 |
| m |
∵PB∥x轴,
∴B点的纵坐标为
| 3 |
| m |
将点B的纵坐标代入反比例函数的解析式y=
| 1 |
| x |
| m |
| 3 |
∴B(
| m |
| 3 |
| 3 |
| m |
| 1 |
| m |
∵PB=m-
| m |
| 3 |
| 2m |
| 3 |
| 3 |
| m |
| 1 |
| m |
| 2 |
| m |
∴S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 2m |
| 3 |
| 2 |
| m |
| 2 |
| 3 |
故答案为
| 2 |
| 3 |
点评:本题考查了反比例函数的综合知识,题目中根据平行坐标轴的直线上的点的坐标特点表示出有关点的坐标是解答本题的关键,难度中等偏上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,以O为圆心,OA长为半径画弧别交OM、ON于A、B两点,再分别以为A、B为圆心,以OA长为半径画弧,两弧交于点C,分别连接AC、BC,则四边形OACB一定是( )
如图,以O为圆心,OA长为半径画弧别交OM、ON于A、B两点,再分别以为A、B为圆心,以OA长为半径画弧,两弧交于点C,分别连接AC、BC,则四边形OACB一定是( )| A、梯形 | B、菱形 | C、矩形 | D、正方形 |
 如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )
如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )| A、115° | B、125° |
| C、135° | D、145° |
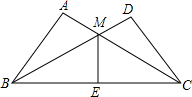 如图,∠ABC=∠DCB,AB=DC,ME平分∠BMC交BC于点E,则下列说法正确的有( )
如图,∠ABC=∠DCB,AB=DC,ME平分∠BMC交BC于点E,则下列说法正确的有( )①△ABC≌△DCB;②ME垂直平分BC;③△ABM≌△EBM;④△ABM≌△DCM.
| A、1个 | B、2个 | C、3个 | D、4个 |
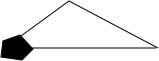 如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( )
如图所示,八年级某同学书上的图形(三角形)不小心被墨迹污染了一部分,但他很快就根据所学知识,画出一个与书上完全一样的三角形,那么这两个三角形全等的依据是( )| A、SSS | B、SAS |
| C、ASA | D、AAS |
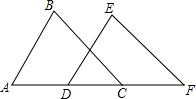 如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由.
如图,已知AB∥DE,BC∥EF,C在AF上,且AD=CF,△ABC与△DEF全等吗?请说明理由. 如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.
如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.