题目内容
 如图,在平面直角坐标系中,直线AB与x轴、y轴分别相交于点A(6,0)、B(0,8).点C(0,m)是线段OB上动点,过点C作CE⊥AB于点E,点D为
如图,在平面直角坐标系中,直线AB与x轴、y轴分别相交于点A(6,0)、B(0,8).点C(0,m)是线段OB上动点,过点C作CE⊥AB于点E,点D为x轴上一动点,连结CD、DE,以CD、DE为边作?CDEF.
(1)求CE的长(用含m的代数式表示);
(2)当m=3时,是否存在点D,使?CDEF得顶点F恰好落在y轴上?若存在,求出点D的坐标;若不存在,请说明理由;
(3)点D在整个运动过程中,若存在唯一的位置,使得?CDEF为矩形,请求出所有满足条件的m的值.
考点:一次函数综合题
专题:
分析:(1)首先证明△BCE∽△BAO,根据两个三角形对应边的比相等,可得答案;
(2)证明△EDA∽△BOA,根据相似三角形对应边的比相等即可求得;
(3)分m>0,m=0,m<0三种情况讨论,当m=0时,一定不成立,当m>0时,分0<m<8和m>8两种情况,根据三角函数定义可求解;当m<0时,分点E与点A重合,点E与点A不重合.
(2)证明△EDA∽△BOA,根据相似三角形对应边的比相等即可求得;
(3)分m>0,m=0,m<0三种情况讨论,当m=0时,一定不成立,当m>0时,分0<m<8和m>8两种情况,根据三角函数定义可求解;当m<0时,分点E与点A重合,点E与点A不重合.
解答:解:(1)∵A(6,0),B(0,8),
∴OA=6,0B=8,
AB=
=10,
∵∠CEB=∠AOB=90°,
∴∠OBA=∠EBC,
∴△BCE∽△BAO,
=
,即
=
,
CE=-
m+
;
(2)∵m=3,
∴BC=8-m=5,CE=-
m+
=3,
∴BE=4,
∵点F落在y轴上,(如图2)
 ,
,
∴DE∥BO,
∴△EDA∽△BOA,
∴
=
,即
=
,
∴OD=
,
点D的坐标为(
,0);
(3)取CE的中点P,过P作PG⊥y轴于G点,
∴CP=
CE=
-
m.
(Ⅰ)当m>0时,
①0<m<8时,如图3,

∠GCP=∠BAO,
cos∠GCP=cos∠BAO=
,
∴CG=CP•cos∠GCP=
(
-
)=
-
m
∴OG=OC+CG=m+
-
m=
m+
,
根据题意,得
OG=CP
∴
m+
=
-
m,
解得m=
,
②当m≥8时,OG>CP显然不存在满足条件的m的值;
(Ⅱ)当m=0时,点C与原点O重合,(图4)
 ;
;
(Ⅲ)当m<0时,
①当点E与点A重合时,如图5,

易证△COA∽△AOB,
∴
=
即
=
,解得m=-
;
②当点E与点A不重合时,如图6,
 ,
,
OG=OC-CG=-m-(
-
m)═-
m-
,
由题意,得
OG=CP
即-
m-
=
-
m,
解得m=-
,
综上所述:m
或0或-
或-
.
∴OA=6,0B=8,
AB=
| OA2+OB2 |
∵∠CEB=∠AOB=90°,
∴∠OBA=∠EBC,
∴△BCE∽△BAO,
| OE |
| OA |
| BC |
| AB |
| CE |
| 6 |
| 8-m |
| 10 |
CE=-
| 3 |
| 5 |
| 24 |
| 5 |
(2)∵m=3,
∴BC=8-m=5,CE=-
| 3 |
| 5 |
| 24 |
| 5 |
∴BE=4,
∵点F落在y轴上,(如图2)
 ,
,∴DE∥BO,
∴△EDA∽△BOA,
∴
| AD |
| AO |
| AE |
| AB |
| 6-OD |
| 6 |
| 6 |
| 10 |
∴OD=
| 12 |
| 5 |
点D的坐标为(
| 12 |
| 5 |
(3)取CE的中点P,过P作PG⊥y轴于G点,
∴CP=
| 1 |
| 2 |
| 12 |
| 5 |
| 3 |
| 10 |
(Ⅰ)当m>0时,
①0<m<8时,如图3,

∠GCP=∠BAO,
cos∠GCP=cos∠BAO=
| 3 |
| 5 |
∴CG=CP•cos∠GCP=
| 3 |
| 5 |
| 12 |
| 5 |
| 3m |
| 10 |
| 36 |
| 25 |
| 9 |
| 50 |
∴OG=OC+CG=m+
| 36 |
| 25 |
| 9 |
| 50 |
| 41 |
| 50 |
| 36 |
| 25 |
根据题意,得
OG=CP
∴
| 41 |
| 50 |
| 36 |
| 25 |
| 12 |
| 5 |
| 3 |
| 10 |
解得m=
| 6 |
| 7 |
②当m≥8时,OG>CP显然不存在满足条件的m的值;
(Ⅱ)当m=0时,点C与原点O重合,(图4)
 ;
;(Ⅲ)当m<0时,
①当点E与点A重合时,如图5,

易证△COA∽△AOB,
∴
| CO |
| AO |
| AO |
| OB |
| -m |
| 6 |
| 6 |
| 8 |
| 9 |
| 2 |
②当点E与点A不重合时,如图6,
 ,
,OG=OC-CG=-m-(
| 36 |
| 25 |
| 9 |
| 50 |
| 41 |
| 50 |
| 36 |
| 25 |
由题意,得
OG=CP
即-
| 41 |
| 50 |
| 36 |
| 25 |
| 12 |
| 5 |
| 3 |
| 10 |
解得m=-
| 96 |
| 13 |
综上所述:m
| 6 |
| 7 |
| 9 |
| 2 |
| 96 |
| 13 |
点评:本题考查了一次函数综合题,(1)利用了相似三角形的判定与性质;(2)利用了平行线截三角形两边所得的三角形与原三角形相似,又利用了对应边的比相等;(3)分类讨论是解题关键,利用了三角函数的定义,相似三角形的性质.

练习册系列答案
相关题目
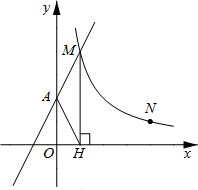 如图,直线y1=2x+2与y轴交于A点,与反比例函数y2=
如图,直线y1=2x+2与y轴交于A点,与反比例函数y2= 以萝卜或马铃薯为主要材料,制作下列两组三视图所表示的几何体的立体模型,并画出你制作的这个模型.
以萝卜或马铃薯为主要材料,制作下列两组三视图所表示的几何体的立体模型,并画出你制作的这个模型.