题目内容
计算:
(1)-(a4)2•(a2)3
(2)|3-
|-
+(
)0.
(3)(x-y)2-(x+y)(x-y)
(4)2006×2008-20072.
(1)-(a4)2•(a2)3
(2)|3-
| 3 |
| 16 |
| 1 |
| 3 |
(3)(x-y)2-(x+y)(x-y)
(4)2006×2008-20072.
考点:整式的混合运算,零指数幂
专题:计算题
分析:(1)原式利用幂的乘方运算法则计算即可得到结果;
(2)原式第一项利用绝对值的代数意义计算,第二项利用平方根定义计算,第三项利用零指数幂法则计算,即可得到结果;
(3)原式利用完全平方公式及平方差公式计算,去括号合并即可得到结果;
(4)原式变形后,利用平方差公式计算即可求出值.
(2)原式第一项利用绝对值的代数意义计算,第二项利用平方根定义计算,第三项利用零指数幂法则计算,即可得到结果;
(3)原式利用完全平方公式及平方差公式计算,去括号合并即可得到结果;
(4)原式变形后,利用平方差公式计算即可求出值.
解答:解:(1)原式=-a14;
(2)原式=3-
-4+1=-
;
(3)原式=x2-2xy+y2-x2+y2=-2xy+2y2;
(4)原式=(2007-1)×(2007+1)-20072=20072-20072-1=-1.
(2)原式=3-
| 3 |
| 3 |
(3)原式=x2-2xy+y2-x2+y2=-2xy+2y2;
(4)原式=(2007-1)×(2007+1)-20072=20072-20072-1=-1.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
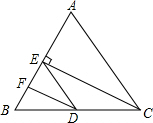 如图所示,在△ABC中,CE⊥AB于点E,点D在BC上,∠BED=∠A,CE平分∠ACB,DF平分∠BDE,求证:DF⊥AB.
如图所示,在△ABC中,CE⊥AB于点E,点D在BC上,∠BED=∠A,CE平分∠ACB,DF平分∠BDE,求证:DF⊥AB.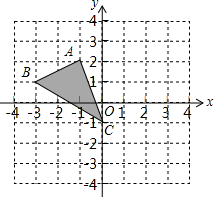 如图,已知△ABC的三个顶点恰好是网格的格点,按照图中的位置建立平面直角坐标系:
如图,已知△ABC的三个顶点恰好是网格的格点,按照图中的位置建立平面直角坐标系: 如图,已知四边形ABED∽四边形BCGF∽四边形CAIH,记四边形ABED、四边形BFGC和四边形CAIH的面积分别为S3、S2、S1,若S1+S2=S3,求证:△ABC为直角三角形.
如图,已知四边形ABED∽四边形BCGF∽四边形CAIH,记四边形ABED、四边形BFGC和四边形CAIH的面积分别为S3、S2、S1,若S1+S2=S3,求证:△ABC为直角三角形. 如图,在平面直角坐标系中,直线AB与x轴、y轴分别相交于点A(6,0)、B(0,8).点C(0,m)是线段OB上动点,过点C作CE⊥AB于点E,点D为
如图,在平面直角坐标系中,直线AB与x轴、y轴分别相交于点A(6,0)、B(0,8).点C(0,m)是线段OB上动点,过点C作CE⊥AB于点E,点D为 如图,AD∥BC,∠DAC=70°,∠ACF=25°,∠EFC=135°,求证:EF∥BC.
如图,AD∥BC,∠DAC=70°,∠ACF=25°,∠EFC=135°,求证:EF∥BC.