题目内容
12.二元一次方程4x+y=10的所有正整数解是$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.分析 把方程化为用一个未知数表示成另一个未知数的形式,再根据x、y均为正整数求解即可.
解答 解:
方程4x+y=10可化为y=10-4x,
∵x、y均为正整数,
∴10-4x>0,
当x=1时,y=6,
当x=2时,y=2,
∴方程4x+y=10的正整数解为:$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=1}\\{y=6}\end{array}\right.$,$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$.
点评 本题主要考查方程的特殊解,用一个未知数表示成另一个未知数是解题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.在同一直角坐标系中,若直线y=kx+3与直线y=-2x+b平行,则( )
| A. | k=-2,b≠3 | B. | k=-2,b=3 | C. | k≠-2,b≠3 | D. | k≠-2,b=3 |
20.抛掷一枚质地均匀的硬币,连续3次都是正面向上,则关于第4次抛掷结果,下面叙述正确的是( )
| A. | P(正面向上)>P(反面向上) | B. | P(正面向上)<P(反面向上) | ||
| C. | P(正面向上)=P(反面向上) | D. | 无法确定 |
17.任意实数a,可用[a]表示不超过a的最大整数,如[4]=4,[$\sqrt{3}$]=1,已知[$\sqrt{n}$]=5,则下列n的值符合条件的是( )
| A. | n=5 | B. | n=18 | C. | n=28 | D. | n=36 |
2.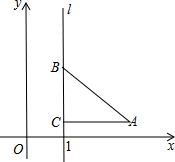 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )
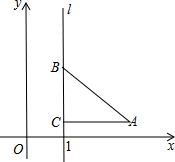 如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )
如图,直线l是经过点(1,0)且与y轴平行的直线.Rt△ABC中直角边AC=4,BC=3.将BC边在直线l上滑动,使A,B在函数y=$\frac{k}{x}$的图象上.那么k的值是( )| A. | 3 | B. | 6 | C. | 12 | D. | $\frac{15}{4}$ |
