题目内容
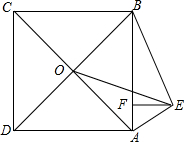 如图,以正方形ABCD的一边AB为斜边向外作Rt△AEB,过点E作EF⊥AB,连接EO
如图,以正方形ABCD的一边AB为斜边向外作Rt△AEB,过点E作EF⊥AB,连接EO(1)若S△AEB=6,EF=2,求正方形ABCD的面积;
(2)求证:∠BEO=∠AEO.
考点:正方形的性质,全等三角形的判定与性质,角平分线的性质
专题:
分析:(1)利用S△AEB的面积列式求出AB,再根据正方形的面积公式列式计算即可得解;
(2)取AB的中点G,根据直角三角形斜边上的中线等于斜边的一半可得OG=EG=AG=BG,然后判断出点A、E、B、O四点共圆,根据同弧所对的圆周角相等可得∠BEO=∠BAO,∠AEO=∠ABO,再根据正方形的每一条对角线平分一组对角可得∠BAO=∠ABO=45°,从而得到∠BEO=∠AEO=45°.
(2)取AB的中点G,根据直角三角形斜边上的中线等于斜边的一半可得OG=EG=AG=BG,然后判断出点A、E、B、O四点共圆,根据同弧所对的圆周角相等可得∠BEO=∠BAO,∠AEO=∠ABO,再根据正方形的每一条对角线平分一组对角可得∠BAO=∠ABO=45°,从而得到∠BEO=∠AEO=45°.
解答: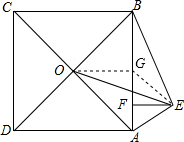 (1)解:∵EF⊥AB,
(1)解:∵EF⊥AB,
∴S△AEB=
AB•EF=
AB•2=6,
解得AB=6,
∴正方形ABCD的面积为62=36;
(2)证明:如图,取AB的中点G,
在正方形ABCD中,AC⊥BD,
∴OG=AG=BG,
∵△AEB是直角三角形,∠AEB=90°,
∴EG=AG=BG,
∴OG=EG=AG=BG,
∴点A、E、B、O四点共圆,
∴BEO=∠BAO,∠AEO=∠ABO,
由正方形的性质,∠BAO=∠ABO=45°,
∴∠BEO=∠AEO=45°,
故:∠BEO=∠AEO.
 (1)解:∵EF⊥AB,
(1)解:∵EF⊥AB,∴S△AEB=
| 1 |
| 2 |
| 1 |
| 2 |
解得AB=6,
∴正方形ABCD的面积为62=36;
(2)证明:如图,取AB的中点G,
在正方形ABCD中,AC⊥BD,
∴OG=AG=BG,
∵△AEB是直角三角形,∠AEB=90°,
∴EG=AG=BG,
∴OG=EG=AG=BG,
∴点A、E、B、O四点共圆,
∴BEO=∠BAO,∠AEO=∠ABO,
由正方形的性质,∠BAO=∠ABO=45°,
∴∠BEO=∠AEO=45°,
故:∠BEO=∠AEO.
点评:本题考查了正方形的性质,三角形的面积,直角三角形斜边上的中线等于斜边的一半的性质,(2)利用四点共圆和同弧所对的圆周角相等的性质求解更简便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列计算正确的是( )
| A、(a+2)(a-2)=a2-2 |
| B、(1+3a)(1-3b)=1-9ab |
| C、(x+1)(x-2)=x2-x-2 |
| D、(x-y)2=x2-y2 |
 如图,直线y1=
如图,直线y1= 快、慢两车分别从相距240千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车早1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.
快、慢两车分别从相距240千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车早1小时到达甲地,快、慢两车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示. 如图,在平面直角坐标系中,正方形OABC的边长是4,点A,C分别在y轴、x轴的正半轴上,动点P从点A开始,以每秒2个单位长度的速度在线段AB上来回运动.动点Q从点B开始沿B→C→O的方向,以每秒1个单位长度的速度向点O运动.P,Q两点同时出发,当点Q到达点O时,两点同时停止运动.设运动时间为t秒.
如图,在平面直角坐标系中,正方形OABC的边长是4,点A,C分别在y轴、x轴的正半轴上,动点P从点A开始,以每秒2个单位长度的速度在线段AB上来回运动.动点Q从点B开始沿B→C→O的方向,以每秒1个单位长度的速度向点O运动.P,Q两点同时出发,当点Q到达点O时,两点同时停止运动.设运动时间为t秒.