题目内容
2.已知关于x的一元二次方程x2-(k+1)x-6=0的一个根为2,求k的值及另一个根.分析 由于一根为2,把x=2代入方程即可求得k的值.然后根据两根之积即可求得另一根.
解答 解:∵方程x2-(k+1)x-6=0的一个根为2,
∴22-2(k+1)-6=0,
解得k=-2,
设另一根为x,
∵2x=-6,
∴x=-3,
∴k=-2,另一根为-3.
点评 考查了一元二次方程的解的知识,解题时可利用根与系数的关系使问题简化,难度不大.

练习册系列答案
相关题目
14.下列根式是最简根式的是( )
| A. | $\sqrt{0.2}$ | B. | $\frac{\sqrt{15}}{3}$ | C. | $\sqrt{{a}^{2}-2ab+{b}^{2}}$ | D. | $\sqrt{18}$ |
15.下列说法不正确的是( )
| A. | 9的算术平方根是3 | B. | $\sqrt{16}$的平方根是±2 | ||
| C. | 27的立方根是±3 | D. | 立方根等于-1的实数是-1 |
17.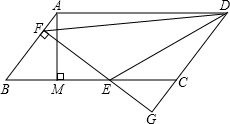 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )
 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )| A. | 20 | B. | 24 | C. | 28 | D. | 36 |
7.下列分式中,是最简分式的是( )
| A. | $\frac{x+1}{2(x+1)}$ | B. | $\frac{x-y}{{x}^{2}-{y}^{2}}$ | C. | $\frac{3{x}^{2}+x}{{x}^{2}}$ | D. | $\frac{x+1}{{x}^{2}+1}$ |
12.设点A(-1,a)和点B(4,b)在直线y=-x+m上,则a与b的大小关系是( )
| A. | a=b | B. | a>b | C. | a<b | D. | 无法确定 |
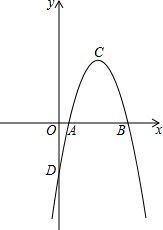 如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D.
如图,在平面直角坐标系中,二次函数y=ax2+bx-7的图象交x轴于A,B两点,交y轴于点D,点C为抛物线的顶点,且A,C两点的横坐标分别为1和4D. 如图,两条直线被三条平行线所截,AB=6,BC=8,DE=4,则DF=$\frac{28}{3}$.
如图,两条直线被三条平行线所截,AB=6,BC=8,DE=4,则DF=$\frac{28}{3}$. 如图,AE交△ABC边BC于点D,∠C=∠E,AD=8,BC=16,若BD:DC=5:3,求DE的长.
如图,AE交△ABC边BC于点D,∠C=∠E,AD=8,BC=16,若BD:DC=5:3,求DE的长.