题目内容
17.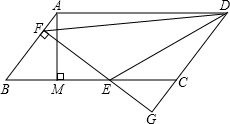 如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )
如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上一个动点(不与B,C重合),过E作直线AB的垂线,垂足为F,FE与DC的延长线相交于点G,连结DE,DF,当点E在线段BC上运动时,△BEF和△CEG的周长之和为( )| A. | 20 | B. | 24 | C. | 28 | D. | 36 |
分析 过点C作FG的平行线交直线AB于H,证得四边形FHCG为矩形.得出FH=CG,FG=CH,所以△BEF与△CEG的周长之和等于BC+CH+BH,证得Rt△BEF∽Rt△BAM,那么根据相似三角形的性质得到$\frac{AB}{BC}$=$\frac{AM}{CH}$,即可求得CH=8,然后根据勾股定理求得BH=6,即可求出两三角形的周长和是24.
解答 解: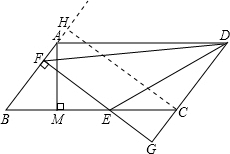 过点C作FG的平行线交直线AB于H,
过点C作FG的平行线交直线AB于H,
因为GF⊥AB,所以四边形FHCG为矩形.
所以FH=CG,FG=CH,
因此,△BEF与△CEG的周长之和等于BC+CH+BH,
∵∠B=∠B,∠AMB=∠BHC=90°
∴△ABM∽△CBH,
∴$\frac{AB}{BC}$=$\frac{AM}{CH}$,
由BC=10,AB=5,AM=4,
∴CH=$\frac{AM•BC}{AB}$=$\frac{4×10}{5}$=8,
在RT△BCH中,BH=$\sqrt{B{C}^{2}-C{H}^{2}}$=6,
所以BC+CH+BH=24,
所以,△BEF与△CEG的周长之和为24;
故选B.
点评 此题主要考查了矩形的判定和性质,相似三角形的判定和性质,勾股定理,熟练掌握相似三角形的判定与性质是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列说法正确的是( )
| A. | 一颗质地均匀的骰子已连续抛投了2015次,其中抛掷出5点的次数最少,则第2016次一定抛掷出5点 | |
| B. | 某种彩票中奖的概率是1%,因此买100张该种彩票一定会中奖 | |
| C. | 天气预报说明天下雨的概率是50%,所以明天将有一半时间在下雨 | |
| D. | 抛掷一枚图钉,钉尖触地和钉尖朝上的概率不相等 |
6.已知$\frac{x}{y}$=$\frac{2}{3}$,则$\frac{x}{x-y}$的值为( )
| A. | -2 | B. | 2 | C. | 3 | D. | -3 |
 如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E,A在直线DC同侧,连接AE.求证:
如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边三角形CDE,使点E,A在直线DC同侧,连接AE.求证: 如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),抛物线y=ax2+bx+c的图象过点C(1,0),并与直线相交于A、B两点.(1)求抛物线和直线AB的函数关系式;
如图,在平面直角坐标系中,直线AB交x轴于点A(-4,0),交y轴于点B(0,2),抛物线y=ax2+bx+c的图象过点C(1,0),并与直线相交于A、B两点.(1)求抛物线和直线AB的函数关系式;