题目内容
9.观察下列各式:1=0+1
2+3+4=1+8
5+6+7+8+9=8+27
10+11+12+12+14+15+16=27+64.
你能做出什么一般性的猜想?能证明你的猜想吗?
分析 首先根据每个算式左边的加数个数分别是1、3、5、7、…,可得第n个算式左边的加数个数是2n-1个;然后根据1=(1-1)2+1,2=(2-1)2+1,5=(3-1)2+1,…,可得第n个算式左边的第一个加数是(n-1)2+1;最后根据0=03,1=13,8=23,27=33,…,判断出第n个算式右边的两个加数分别是(n-1)3、n3,据此总结出一般性的猜想,再根据等差数列的求和公式以及立方和公式证明即可.
解答 解:因为1=0+1
2+3+4=1+8
5+6+7+8+9=8+27
10+11+12+12+14+15+16=27+64
…,
所以做出的一般性的猜想为:
[(n-1)2+1]+[(n-1)2+2]+[(n-1)2+3]+[(n-1)2+4]+…+n2=(n-1)3+n3;
证明:因为[(n-1)2+1]+[(n-1)2+2]+[(n-1)2+3]+[(n-1)2+4]+…+n2
=[(n-1)2+1+n2]×(2n-1)÷2
=2(n2-n+1)×(2n-1)÷2
=(n2-n+1)×(2n-1)
=[(n-1)+n]×[(n-1)2-n(n-1)+n2]
=(n-1)3+n3
所以[(n-1)2+1]+[(n-1)2+2]+[(n-1)2+3]+[(n-1)2+4]+…+n2=(n-1)3+n3成立.
点评 (1)此题主要考查了探寻数字规律问题,注意观察总结规律,并能正确的应用规律,解答此题的关键是判断出:[(n-1)2+1]+[(n-1)2+2]+[(n-1)2+3]+[(n-1)2+4]+…+n2=(n-1)3+n3.
(2)此题还考查了等差数列的求和的方法,以及立方和公式的应用,要熟练掌握.

练习册系列答案
相关题目
17.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A. | 1:2:3:4 | B. | 1:2:1:2 | C. | 2:2:1:1 | D. | 1:2:2:1 |
18.以下说法正确的是( )
| A. | 在367人中至少有两个人的生日相同 | |
| B. | 一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 | |
| C. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| D. | 一个不透明的袋中装有3个红球,5个白球,搅匀后想中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性 |
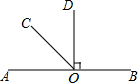 如图,O是直线AB上的一点,且∠AOC=$\frac{1}{3}$∠BOC.
如图,O是直线AB上的一点,且∠AOC=$\frac{1}{3}$∠BOC.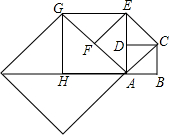 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.
如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形,再以对角线AE为边作第三个正方形AEGH,如此下去,第n个正方形的边长为($\sqrt{2}$)n-1.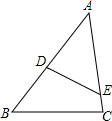 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5.