题目内容
小明和同桌小聪在课后做作业时,对课本中的一道作业题,进行了认真探索.
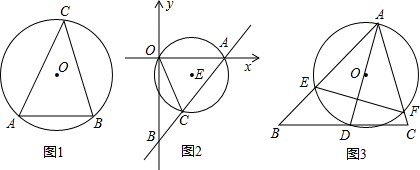
【作业题】如图1,一个半径为100m的圆形人工湖如图所示,弦AB是湖上的一座桥,测得圆周角∠C=45°,求桥AB的长.
小明和小聪经过交流,得到了如下的两种解决方法:
方法一:延长BO交⊙O与点E,连接AE,得 Rt△ABE,∠E=∠C,∴AB=100
;
方法二:作AB的弦心距OH,连接OB,∴∠BOH=∠C,解Rt△OHB,∴HB=50
,
∴AB=100
.
感悟:圆内接三角形的一边和这边的对锐角、圆的半径(或直径)这三者关系,可构成直角三角形,从而把一边和这边的对锐角﹑半径建立一个关系式.
(1)问题解决:受到(1)的启发,请你解下面命题:
如图2,点A(3,0)、B(0,-3
),C为直线AB上一点,过A、O、C的⊙E的半径为2.求线段OC的长.
(2)问题拓展:如图3,△ABC中,∠ACB=75°,∠ABC=45°,AB=2
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连结EF,设⊙O半径为x,EF为y.
①y关于x的函数关系式;②求线段EF长度的最小值.

【作业题】如图1,一个半径为100m的圆形人工湖如图所示,弦AB是湖上的一座桥,测得圆周角∠C=45°,求桥AB的长.
小明和小聪经过交流,得到了如下的两种解决方法:
方法一:延长BO交⊙O与点E,连接AE,得 Rt△ABE,∠E=∠C,∴AB=100
| 2 |
方法二:作AB的弦心距OH,连接OB,∴∠BOH=∠C,解Rt△OHB,∴HB=50
| 2 |
∴AB=100
| 2 |
感悟:圆内接三角形的一边和这边的对锐角、圆的半径(或直径)这三者关系,可构成直角三角形,从而把一边和这边的对锐角﹑半径建立一个关系式.
(1)问题解决:受到(1)的启发,请你解下面命题:
如图2,点A(3,0)、B(0,-3
| 3 |
(2)问题拓展:如图3,△ABC中,∠ACB=75°,∠ABC=45°,AB=2
| 2 |
①y关于x的函数关系式;②求线段EF长度的最小值.
考点:圆的综合题
专题:
分析:(1)先根据锐角三角函数的定义求出∠OAB的度数,延长OE交⊙O于点F,连接CF,根据圆周角定理可得出∠F=∠OAB=60°,再由锐角三角函数的定义即可得出结论;
(2)①先根据三角形内角和定理得出∠BAC=60°,延长EO交⊙O于点G,连接GF,根据锐角三角函数的定义即可得出结论;
②作AH⊥BC于点H,根据勾股定理求出AH的长,再根据AD=EG=2x得出x的取值范围,进而得出结论.
(2)①先根据三角形内角和定理得出∠BAC=60°,延长EO交⊙O于点G,连接GF,根据锐角三角函数的定义即可得出结论;
②作AH⊥BC于点H,根据勾股定理求出AH的长,再根据AD=EG=2x得出x的取值范围,进而得出结论.
解答: 解:(1)∵tan∠OAB=
解:(1)∵tan∠OAB=
=
,
∴∠OAB=60°,
延长OE交⊙O于点F,连接CF,
∴∠F=∠OAB=60°,
∴OC=2
;
(2)①∵∠ACB=75°,∠ABC=45°,
∴∠BAC=60°,
如图3,延长EO交⊙O于点G.连接GF,
∴y=
x;
②如图3,作AH⊥BC于点H,
∵Rt△ABH中,∠ABC=45°,AB=2
,
∴AH=2,
∵AD=EG=2x,
∴2≤AD≤2
,即1≤x≤
,
∴y的最小值为
.
 解:(1)∵tan∠OAB=
解:(1)∵tan∠OAB=| OB |
| OA |
| 3 |
∴∠OAB=60°,
延长OE交⊙O于点F,连接CF,
∴∠F=∠OAB=60°,
∴OC=2
| 3 |
(2)①∵∠ACB=75°,∠ABC=45°,
∴∠BAC=60°,
如图3,延长EO交⊙O于点G.连接GF,
∴y=
| 3 |
②如图3,作AH⊥BC于点H,
∵Rt△ABH中,∠ABC=45°,AB=2
| 2 |
∴AH=2,
∵AD=EG=2x,
∴2≤AD≤2
| 2 |
| 2 |
∴y的最小值为
| 3 |
点评:本题考查的是圆的综合题,涉及到圆周角定理、直角三角形的性质等知识,难度适中.

练习册系列答案
相关题目
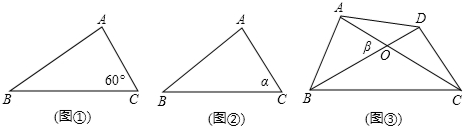

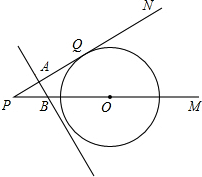 如图,已知⊙O的圆心O在射线PM上,PN切⊙O于Q,PO=20cm,∠P=30°,A、B两点同时从P点出发,点A沿PN方向移动,点B以4cm/s的速度沿PM方向移动,且直线AB始终垂直PN.设运动时间为t秒,求下列问题.(结果保留根号)
如图,已知⊙O的圆心O在射线PM上,PN切⊙O于Q,PO=20cm,∠P=30°,A、B两点同时从P点出发,点A沿PN方向移动,点B以4cm/s的速度沿PM方向移动,且直线AB始终垂直PN.设运动时间为t秒,求下列问题.(结果保留根号)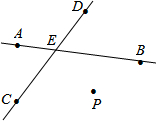 如图,直线CD与直线AB相交于E,根据下列语句画图.
如图,直线CD与直线AB相交于E,根据下列语句画图. 一个盒子里装有分别标有数字-2、-1、0、1、2、的五个光滑小球,这五个小球除标的数字外其余完全相同.现从该盒子中随机摸出一个小球其数字记为m,放回后再随机摸出一个小球其数字记为n.如图,在平面直角坐标系内,则点(m,n)恰好落在以点A(0,3)、B(2,0)、C(0,-2)、D(-2,0)为顶点的四形ABCD内部(不含边界)的概率是
一个盒子里装有分别标有数字-2、-1、0、1、2、的五个光滑小球,这五个小球除标的数字外其余完全相同.现从该盒子中随机摸出一个小球其数字记为m,放回后再随机摸出一个小球其数字记为n.如图,在平面直角坐标系内,则点(m,n)恰好落在以点A(0,3)、B(2,0)、C(0,-2)、D(-2,0)为顶点的四形ABCD内部(不含边界)的概率是