题目内容
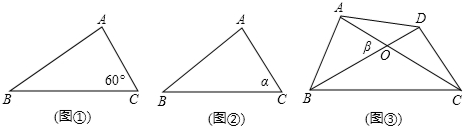
(1)如图①,若BC=6,AC=4,∠C=60°,求△ABC的面积S△ABC;
(2)如图②,若BC=a,AC=b,∠C=α,求△ABC的面积S△ABC;
(3)如图③,四边形ABCD,AC=m,BD=n,对角线AC交于O点,他们所成锐角为β,求四边形ABCD的面积S四边形ABCD.
(2)如图②,若BC=a,AC=b,∠C=α,求△ABC的面积S△ABC;
(3)如图③,四边形ABCD,AC=m,BD=n,对角线AC交于O点,他们所成锐角为β,求四边形ABCD的面积S四边形ABCD.

考点:解直角三角形
专题:
分析:(1)过A作AM⊥BC于M,解直角三角形求出AM,再根据三角形面积公式求出即可;
(2)过A作AM⊥BC于M,解直角三角形求出AM,再根据三角形面积公式求出即可;
(3)过A作AE⊥BD于E,过C作CF⊥BD于F,解直角三角形求出AE、CF,根据三角形面积公式求出即可.
(2)过A作AM⊥BC于M,解直角三角形求出AM,再根据三角形面积公式求出即可;
(3)过A作AE⊥BD于E,过C作CF⊥BD于F,解直角三角形求出AE、CF,根据三角形面积公式求出即可.
解答:解: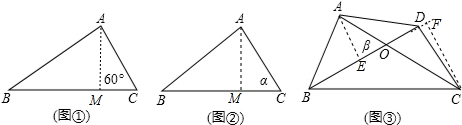
(1)如图①,过A作AM⊥BC于M,
则∠AMC=90°,
∵∠C=60°,AC=4,
∴AM=AC×sin60°=4×
=2
,
∵BC=6,
∴△ABC的面积S△ABC=
×BC×AM=
×6×2
=6
;
(2)如图②,过A作AM⊥BC于M,
则∠AMC=90°,
∵∠C=α,AC=b,
∴AM=AC×sinα=b×sinα=bsinα,
∵BC=a,
∴△ABC的面积S△ABC=
×BC×AM=
×a×bsinα=
absinα;
(3)如图3,过A作AE⊥BD于E,过C作CF⊥BD于F,BD=n,OA+OC=m,
∵AC、BD夹角为β,
∴AE=OA•sinβ,CF=OC•sinβ,
∴S四边形ABCD=S△ABD+S△BDC
=
BD•AE+
BD•CF
=
BD•(AE+CF)
=
BD•(OA•sinβ+OC•sinβ)=
BD•AC•sinβ=
mnsinβ.
即四边形ABCD的面积S四边形ABCD=
mnsinβ.

(1)如图①,过A作AM⊥BC于M,
则∠AMC=90°,
∵∠C=60°,AC=4,
∴AM=AC×sin60°=4×
| ||
| 2 |
| 3 |
∵BC=6,
∴△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
(2)如图②,过A作AM⊥BC于M,
则∠AMC=90°,
∵∠C=α,AC=b,
∴AM=AC×sinα=b×sinα=bsinα,
∵BC=a,
∴△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图3,过A作AE⊥BD于E,过C作CF⊥BD于F,BD=n,OA+OC=m,
∵AC、BD夹角为β,
∴AE=OA•sinβ,CF=OC•sinβ,
∴S四边形ABCD=S△ABD+S△BDC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即四边形ABCD的面积S四边形ABCD=
| 1 |
| 2 |
点评:本题考查了解直角三角形,三角形的面积的应用,此题比较难,解题时关键要找对思路,即原四边形的高已经发生了变化,只要把高求出来,一切将迎刃而解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 已知:直线
已知:直线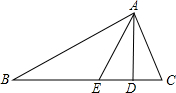 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.