题目内容
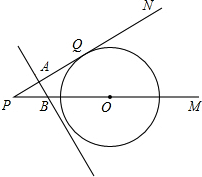 如图,已知⊙O的圆心O在射线PM上,PN切⊙O于Q,PO=20cm,∠P=30°,A、B两点同时从P点出发,点A沿PN方向移动,点B以4cm/s的速度沿PM方向移动,且直线AB始终垂直PN.设运动时间为t秒,求下列问题.(结果保留根号)
如图,已知⊙O的圆心O在射线PM上,PN切⊙O于Q,PO=20cm,∠P=30°,A、B两点同时从P点出发,点A沿PN方向移动,点B以4cm/s的速度沿PM方向移动,且直线AB始终垂直PN.设运动时间为t秒,求下列问题.(结果保留根号)(1)求PQ的长;
(2)当t为何值时直线AB与⊙O相切?
考点:切线的判定与性质,勾股定理
专题:
分析:(1)根据切线的性质,可得OQ⊥PN,根据直角三角形的性质、勾股定理,可得答案;
(2)分类讨论,根据勾股定理,可得BP、AB、AP的关系,根据切线的性质,可得矩形,根据矩形的性质,可得AQ的长度,根据线段的和差,可得答案.
(2)分类讨论,根据勾股定理,可得BP、AB、AP的关系,根据切线的性质,可得矩形,根据矩形的性质,可得AQ的长度,根据线段的和差,可得答案.
解答:(1)解:连结OQ
∵PN与⊙O相切于点Q
∴OQ⊥PN
∵∠P=30°,OP=20
∴OQ=10,
在Rt△OPQ中,PQ=
=
=10
(cm);
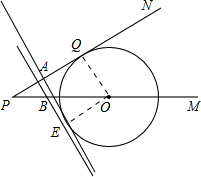
(2)解:设运动t秒
BP=4t,则AB=2t,AP=2
t
①如图,当AB与⊙O切于点E时,连结OE
∴OE⊥AB,
又∵OQ⊥PN,AB⊥PN
∴四边形AEOQ是矩形
∴OE=AQ=10
∴10
-2
t=10,t=
,
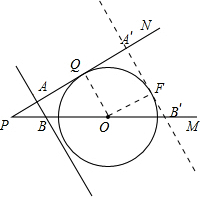
②如图,当A′B′与⊙O相切于点F时,连结OF
∴OF⊥A′B′
又∵OQ⊥PN,AB⊥PN
∴四边形A′FOQ是矩形
∴OF=A′Q,
∵A′P-PQ=A′Q
∴2
t-10
=10,t=
∴当t为
秒或
秒时,直线AB与⊙O相切.
∵PN与⊙O相切于点Q
∴OQ⊥PN
∵∠P=30°,OP=20
∴OQ=10,
在Rt△OPQ中,PQ=
| PO2-OQ2 |
| 202-102 |
| 3 |

(2)解:设运动t秒
BP=4t,则AB=2t,AP=2
| 3 |
①如图,当AB与⊙O切于点E时,连结OE
∴OE⊥AB,
又∵OQ⊥PN,AB⊥PN
∴四边形AEOQ是矩形
∴OE=AQ=10
∴10
| 3 |
| 3 |
15-5
| ||
| 3 |

②如图,当A′B′与⊙O相切于点F时,连结OF
∴OF⊥A′B′
又∵OQ⊥PN,AB⊥PN
∴四边形A′FOQ是矩形
∴OF=A′Q,
∵A′P-PQ=A′Q
∴2
| 3 |
| 3 |
15+5
| ||
| 3 |
∴当t为
15-5
| ||
| 3 |
15+5
| ||
| 3 |
点评:本题考查了切线的性质与判定,利用切线的性质,矩形的性质,线段的和差解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
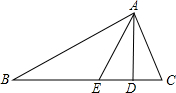 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.
 邻居李大叔在自家后院种了一块长20米,宽16米的长方形菜地,准备修筑两条横竖方向互相垂直的小路,路宽2米,则种植蔬菜的面积为
邻居李大叔在自家后院种了一块长20米,宽16米的长方形菜地,准备修筑两条横竖方向互相垂直的小路,路宽2米,则种植蔬菜的面积为