题目内容
14．小明家承包了一个矩形鱼池，已知其面积为48m2，其对角线长为10m，为建栅栏，要计算这个矩形鱼池的周长，请帮助小明算一算这个矩形的周长．分析 根据矩形的面积公式得到长与宽的积，再根据勾股定理得到长与宽的平方和．联立解方程组求得长与宽的和可．
解答 解：设该矩形相邻两边长为xm，ym，
则 $\left\{\begin{array}{l}{xy=48}\\{{x}^{2}+{y}^{2}=1{0}^{2}}\end{array}\right.$
即x+y=14，
该矩形的周长为14×2=28m，
答：该矩形的周长为28m．
点评 本题主要考查了方程的应用，解题的关键是用x和y表示出对角线的长度，进而求出x+y的值，此题难度不大．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
2．如果$\sqrt{{a}^{2}}$-a=b成立，且b＞0，则a取值范围是（ ）
| A． | a＜0 | B． | a＞0 | C． | a≥0 | D． | 无法确定 |
6．
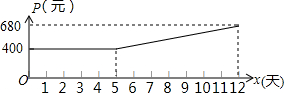某市制药厂需要紧急生产一批药品，要求必须在12天（含12天）内完成．为了加快生产，车间采取工人加班，机器不停的生产方式，这样每天药品的产量y（吨）是时间x（天）一次函数，且满足表中所对应的数量关系．由于机器负荷运转产生损耗，平均生产每吨药品的成本P（元）与时间x（天）的关系满足图中的函数图象．
（1）求药品每天的产量y（吨）是时间x（天）之间的函数关系式；
（2）当5≤x≤12时，直接写出P（元）与时间x（天）的函数关系是P=P=40x+200；
（3）若这批药品的价格为1400元/吨，每天的利润设为W元，求哪一天的利润最高，最高利润是多少？（利润=价格-成本）
（4）为了提高工人加班的津贴，药厂决定在（3）中价格的基础上每吨药品加价a元，但必须满足从第5天到第12天期间，每吨加价a后每天的利润随时间的增大而增大，直线写出a的最小值．
某市制药厂需要紧急生产一批药品，要求必须在12天（含12天）内完成．为了加快生产，车间采取工人加班，机器不停的生产方式，这样每天药品的产量y（吨）是时间x（天）一次函数，且满足表中所对应的数量关系．由于机器负荷运转产生损耗，平均生产每吨药品的成本P（元）与时间x（天）的关系满足图中的函数图象．| 时间x（天） | 2 | 4 |
| 每天产量y（吨） | 24 | 28 |
（2）当5≤x≤12时，直接写出P（元）与时间x（天）的函数关系是P=P=40x+200；
（3）若这批药品的价格为1400元/吨，每天的利润设为W元，求哪一天的利润最高，最高利润是多少？（利润=价格-成本）
（4）为了提高工人加班的津贴，药厂决定在（3）中价格的基础上每吨药品加价a元，但必须满足从第5天到第12天期间，每吨加价a后每天的利润随时间的增大而增大，直线写出a的最小值．
4．若am=2，an=3，则a2m-n的值为（ ）
| A． | 12 | B． | $\frac{4}{3}$ | C． | 1 | D． | $\frac{3}{4}$ |