题目内容
18.从地面垂直向上抛出一小球,小球的高度h(米)与小球运动时间t(秒)的函数关系式是h=9.8t-4.9t2,小球的最大高度为4.9米.分析 把抛物线解析式化成顶点式,即可解答.
解答 解:h=9.8t-4.9t2
=4.9[-(t-1)2+1]=-4.9(x-1)2+4.9,
当t=1时,
函数的最大值为4.9米,
这就是小球运动最大高度,
故答案为:4.9.
点评 本题涉及二次函数的实际应用,难度中等,熟练掌握求二次函数的最值是解题的关键.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
6.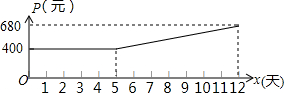 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
(1)求药品每天的产量y(吨)是时间x(天)之间的函数关系式;
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=P=40x+200;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格-成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
 某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.
某市制药厂需要紧急生产一批药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量y(吨)是时间x(天)一次函数,且满足表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本P(元)与时间x(天)的关系满足图中的函数图象.| 时间x(天) | 2 | 4 |
| 每天产量y(吨) | 24 | 28 |
(2)当5≤x≤12时,直接写出P(元)与时间x(天)的函数关系是P=P=40x+200;
(3)若这批药品的价格为1400元/吨,每天的利润设为W元,求哪一天的利润最高,最高利润是多少?(利润=价格-成本)
(4)为了提高工人加班的津贴,药厂决定在(3)中价格的基础上每吨药品加价a元,但必须满足从第5天到第12天期间,每吨加价a后每天的利润随时间的增大而增大,直线写出a的最小值.
7.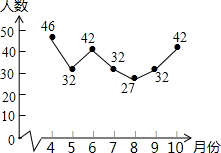 在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
 在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )
在倡导“全民阅读”的环境下,越来越多的学生选择去图书馆借阅图书,小红根据去年4~10月本班同学去图书馆借阅图书的人数,绘制了如果所示的折线统计图,则这些人数的众数是( )| A. | 46人 | B. | 42人 | C. | 32人 | D. | 27人 |
8.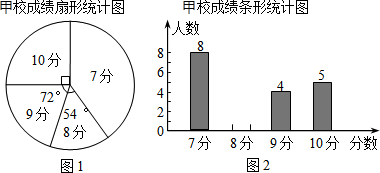 甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
乙校成绩统计表
(1)在图1中,“7分”所在扇形的圆心角等于144度;
(2)请将图2的统计图和乙校成绩统计表补充完整;
(3)成绩最好的男同学王东、李亮.女同学张梅、萧红被选中参加电视辩论,辩论前抽签决定每两人为一组,请你用树状图和列表法表示所有可能的分组结果,并计算两名男同学恰好在同一组的概率.
 甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表
甲、乙两校选派相同人数的学生参加市初中历史知识竞赛,统计结果,发现学生成绩分别为7分、8分、9分、10分(满分10分),依据统计数据绘制了如下尚不完整的统计图表乙校成绩统计表
| 分数 | 7分 | 8分 | 9分 | 10分 |
| 人数 | 11 | 0 | 8 |
(2)请将图2的统计图和乙校成绩统计表补充完整;
(3)成绩最好的男同学王东、李亮.女同学张梅、萧红被选中参加电视辩论,辩论前抽签决定每两人为一组,请你用树状图和列表法表示所有可能的分组结果,并计算两名男同学恰好在同一组的概率.
 如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,当AD=20m时,矩形场地的面积最大.
如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地,当AD=20m时,矩形场地的面积最大.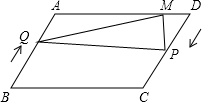 已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).
已知在?ABCD中,AB=20cm,AD=30cm,∠ABC=60°,点Q从点B出发沿BA向点A匀速运动,速度为2cm/s,同时点P从点D出发沿DC匀速运动,速度为3cm/s,当点P停止运动时,点Q也随之停止运动,过点P做PM⊥AD于点M,连接PQ、QM.设运动的时间为ts(0<t≤6).