题目内容
19．
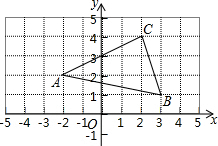如图，边长为1的正方形网格中有格点△ABC和格点O，若把△ABC绕着点O逆时针旋转180°（1）在网格中画出△ABC旋转后的△A1B1C1，并写出B1的坐标．
（2）在网格中画出以O为位似中心，将△ABC按1：2放大的△A2B2C2，并写出B2的坐标．
分析 （1）直接利用旋转的性质分别得出对应点位置进而得出答案；
（2）利用位似图形的性质得出对应点位置进而得出答案．
解答 
解：（1）如图所示：△A1B1C1，即为所求，
B1的坐标为：（-3，-1）；
（2）如图所示：△A2B2C2，即为所求，
B2的坐标为：（6，2）．
点评 此题主要考查了旋转变换和位似变换，根据题意得出对应点位置是解题关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
9．有一种长方体集装箱，其内空长为5米，高4.5米，宽3.4米，用这样的集装箱运长为5米，横截面的外圆直径为0.8米的圆柱形钢管，最多能运（ ）根．
| A． | 20根 | B． | 21根 | C． | 24根 | D． | 25根 |
10．用配方法解方程x2+4x-6=0，下列配方正确的是（ ）
| A． | （x+4）2=22 | B． | （x+2）2=10 | C． | （x+2）2=8 | D． | （x+2）2=6 |
11．下列各题计算正确的是（ ）
| A． | （ab-1）（-4ab2）=-4a2b3-4ab2 | B． | （3x2+xy-y2）•3x2=9x4+3x3y-y2 | ||
| C． | （-3a）（a2-2a+1）=-3a3+6a2 | D． | （-2x）（3x2-4x-2）=-6x3+8x2+4x |
8．若（x2+m）（x2+$\frac{1}{3}$）中不含x2项，则m的值为（ ）
| A． | $\frac{1}{3}$ | B． | 3 | C． | -$\frac{1}{3}$ | D． | -3 |