��Ŀ����
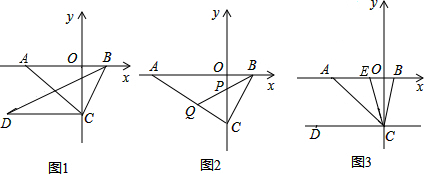
11����ͼ1����ƽ��ֱ������ϵ�У���AΪx�Ḻ������һ�㣬��BΪx����������һ�㣬C��0��a����D��b��a��������a��b�����ϵʽ��|a+3|+��b-a+1��2=0����1��a=-3��b=-4����BCD�����Ϊ6��
��2����ͼ2����AC��BC����P�߶�OC��һ�㣬����BP���ӳ�BP��AC�ڵ�Q������CPQ=��CQPʱ����֤��BPƽ�֡�ABC��
��3����ͼ3����AC��BC����E�ǵ�A���B֮��һ���㣬����CE��CBʼ��ƽ�֡�ECF������E�ڵ�A���B֮���˶�ʱ��$\frac{��BEC}{��BCO}$��ֵ�Ƿ�仯�������䣬�����ֵ�����仯����˵�����ɣ�
���� ��1�����CD�ij��ȣ��ٸ��������ε������ʽ��ʽ���㼴�ɵý⣻
��2�����ݵȽǵ������Ƚ�ɣ�
��3������֤����ACD=��ACE���Ƴ���DCE=2��ACD����֤����ACD=��BCO����BEC=��DCE=2��ACD���ɽ�����⣻
��� ��1���⣺��ͼ1�У�
��|a+3|+��b-a+1��2=0��
��a=-3��b=4��
�ߵ�C��0��-3����D��-4��-3����
��CD=4����CD��x�ᣬ
���BCD�����=$\frac{1}{2}$��4��3=6��
�ʴ�Ϊ-3��-4��6��
��2��֤������ͼ2�У�
�ߡ�CPQ=��CQP=��OPB��AC��BC��
���CBQ+��CQP=90�㣬
�֡ߡ�ABQ+��CPQ=90�㣬
���ABQ=��CBQ��
��BQƽ�֡�CBA��
��3���⣺��ͼ3�У����ۣ�$\frac{��BEC}{��BCO}$=��ֵ=2��
���ɣ���AC��BC��
���ACB=90�㣬
���ACD+��BCF=90�㣬
��CBƽ�֡�ECF��
���ECB=��BCF��
���ACD+��ECB=90�㣬
�ߡ�ACE+��ECB=90�㣬
���ACD=��ACE��
���DCE=2��ACD��
�ߡ�ACD+��ACO=90�㣬��BCO+��ACO=90�㣬
���ACD=��BCO��
��C��0��-3����D��-4��-3����
��CD��AB��
��BEC=��DCE=2��ACD��
���BEC=2��BCO��
��$\frac{��BEC}{��BCO}$=2��
���� ���⿼����������ͼ�����ʣ������εĽ�ƽ���ߣ������ε�����������ε��ڽǺͶ����������ε�������ʵ�֪ʶ��������ʲ�ȷʶͼ�ǽ���Ĺؼ���

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
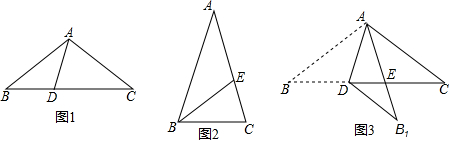
������ʱ����ҵ����ϵ�д� ��ͼ���ڡ�ABC�У�DE��BC����AD=3��BD=4��BC=5����DE�ij�Ϊ��������
��ͼ���ڡ�ABC�У�DE��BC����AD=3��BD=4��BC=5����DE�ij�Ϊ��������| A�� | $\frac{15}{4}$ | B�� | $\frac{15}{7}$ | C�� | $\frac{12}{5}$ | D�� | $\frac{5}{2}$ |
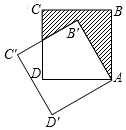 ��ͼ���߳�Ϊ2��������ABCD�Ƶ�A��ʱ����ת30�㵽������AB��C��D�䣬ͼ����Ӱ���ֵ����Ϊ��������
��ͼ���߳�Ϊ2��������ABCD�Ƶ�A��ʱ����ת30�㵽������AB��C��D�䣬ͼ����Ӱ���ֵ����Ϊ��������| A�� | 2 | B�� | $\frac{3\sqrt{3}}{2}$ | C�� | 4-$\frac{4\sqrt{3}}{3}$ | D�� | 4-$\frac{3\sqrt{3}}{4}$ |
��1����һ�ྺ���ɼ�ͳ��ͼ����������
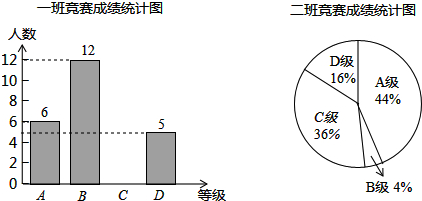
��2�������
| ƽ�������֣� | ��λ�����֣� | �������֣� | |
| һ�� | 87.6 | 90 | 90 |
| ���� | 87.6 | 80 | 100 |
 ����ͼ��ʾ�������������У�ÿ��С�����εı߳���Ϊ1����ABC�Ķ���A��C������ֱ�Ϊ��-4��5������-1��3����
����ͼ��ʾ�������������У�ÿ��С�����εı߳���Ϊ1����ABC�Ķ���A��C������ֱ�Ϊ��-4��5������-1��3����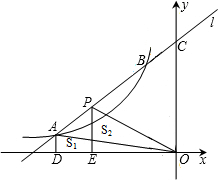 ֱ��l��y���ڵ�C����˫����y=$\frac{k}{x}$��k��0������A��B���㣬P���߶�AB�ϵĵ㣨����A��B�غϣ�������A��P�ֱ���x�������ߣ�����ֱ�ΪD��E������OA��OP�����AOD�����ΪS1����POE�����ΪS2����S1��S2�Ĵ�С��ϵΪS1��S2���á��������ӣ���
ֱ��l��y���ڵ�C����˫����y=$\frac{k}{x}$��k��0������A��B���㣬P���߶�AB�ϵĵ㣨����A��B�غϣ�������A��P�ֱ���x�������ߣ�����ֱ�ΪD��E������OA��OP�����AOD�����ΪS1����POE�����ΪS2����S1��S2�Ĵ�С��ϵΪS1��S2���á��������ӣ���