题目内容
16.一辆汽车油箱现有汽油50L,已知该车平均耗油量为0.1L/km,油箱中的存油量为y(单位:L),行驶里程为x(单位:km),y随着x的变化而变化.(1)写出表示y与x的函数关系的式子;
(2)说出自变量的取值范围;
(3)汽车行驶200km时,油箱中还有多少汽油?
分析 (1)每行程xkm,耗油0.1xl,即总油量减少0.1x,则油箱中的油剩下50-0.1x.
(2)从实际出发,x代表的实际意义为行驶里程,所以x不能为负数,又行驶中的耗油量为0.11x,不能超过油箱中的汽油量50L.
(3)将x=200时,代入第一问中求出的x,y的关系式即可得出答案.
解答 解:(1)根据题意,每行程xkm,耗油0.1xl,即总油量减少0.1x,
则油箱中的油剩下50-0.1x,
故y与x的函数关系式为:y=50-0.1x;
(2)因为x代表的实际意义为行驶里程,所以x不能为负数,即x≥0;
又行驶中的耗油量为0.1x,不能超过油箱中现有汽油量的值50,
即0.1x≤50,解得x≤500.
综上所述,自变量x的取值范围是0≤x≤500;
(3)当x=200时,代入x,y的关系式:y=50-0.1×200=30.
所以,汽车行驶200km时,油桶中还有30L汽油.
点评 本题考查了一次函数的应用,难度不大,但比较繁琐,尤其是第二问要从实际考虑得出x的范围.

练习册系列答案
相关题目
7.下列各组中,是同类项的是( )
| A. | 2与52 | B. | 2abc与-3ac | C. | -2xy与-2ab | D. | 3x2y与3xy2 |
1.下列叙述中错误的是( )
| A. | 两个正方形是相似图形 | |
| B. | 两个菱形是相似图形 | |
| C. | 底角相等的两个等腰三角形是相似图形 | |
| D. | 顶角相等的两个等腰三角形是相似图形 |
6.若关于x的一元二次方程(a+1)x2+x+a2-1=0的一个根是0,则这个方程的另一个根是( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | 1 | D. | -1 |
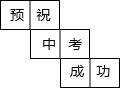
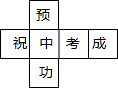
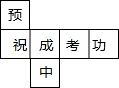
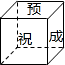 李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )
李明为好友制作一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,期中“预”的对面是“中”,“正”的对面是“功”,则它的平面展开图可能是( )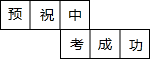
 如图,两条直线a,b相交于O,若∠α=60°,则∠β=120°.
如图,两条直线a,b相交于O,若∠α=60°,则∠β=120°. 如图,在矩形纸片ABCD中,AB=6cm,点E在BC上,且AE=CE,若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=12cm.
如图,在矩形纸片ABCD中,AB=6cm,点E在BC上,且AE=CE,若将纸片沿AE折叠,点B恰好与AC上的点B1重合,则AC=12cm. 如图,已知点B,C,D是线段AE上的点,若AB=BC=CE,D是CE的中点,BD=6,则线段AE=12.
如图,已知点B,C,D是线段AE上的点,若AB=BC=CE,D是CE的中点,BD=6,则线段AE=12.