题目内容
6.当x=$\sqrt{3}$+1,y=$\sqrt{3}$-1时,$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-{y}^{2}}$=$\frac{\sqrt{3}}{3}$.分析 原式约分得到结果,把x与y的值代入计算即可求出值.
解答 解:原式=$\frac{(x-y)^{2}}{(x+y)(x-y)}$=$\frac{x-y}{x+y}$,
当x=$\sqrt{3}$+1,y=$\sqrt{3}$-1时,原式=$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.纳米如同厘米、分米和米一样,是长度的度量单位,原称毫微米,也就是十亿分之一米(即10-9米),那么0.15纳米用科学记数法表示是( )米.
| A. | 0.15×10-9 | B. | 1.5×10-10 | C. | 1.5×10-9 | D. | 0.15×10-10 |
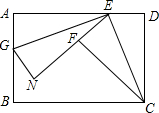 如图,在矩形ABCD中,E为AD边上一点,且AE=AB,把△CDE沿CE边翻折,点D落在点F处,G在AB边上,把△AEG沿EG边翻折,点A刚好落在EF的延长线上N点处.若BG=3,则FN的长为3.
如图,在矩形ABCD中,E为AD边上一点,且AE=AB,把△CDE沿CE边翻折,点D落在点F处,G在AB边上,把△AEG沿EG边翻折,点A刚好落在EF的延长线上N点处.若BG=3,则FN的长为3.




