题目内容
5．
如图，已知点B，C，D是线段AE上的点，若AB=BC=CE，D是CE的中点，BD=6，则线段AE=12．
分析 由已知条件知BC=$\frac{2}{3}$BD，AE=3BC，故AE可求．
解答 解：∵D是CE的中点，AB=BC=CE
∴CD=0.5CE=0.5BC
∴BC=$\frac{2}{3}$BD=4
∴AE=3BC=12．
故答案为：12．
点评 本题考查了两点间的距离，在一条直线或线段上的线段的加减运算和倍数运算，首先明确线段间的相互关系，再根据题意进行计算，利用中点性质转化线段之间的倍分关系是解题的关键．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
10．
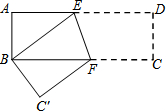将矩形纸片ABCD按如图方式折叠，使点D与点B重合，点C落在点C′处．折痕为EF，若S△ABE：S四边形ABFE=4：9，则cos∠BEF=（ ）
将矩形纸片ABCD按如图方式折叠，使点D与点B重合，点C落在点C′处．折痕为EF，若S△ABE：S四边形ABFE=4：9，则cos∠BEF=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{3\sqrt{10}}{10}$ | C． | 3 | D． | $\frac{\sqrt{10}}{10}$ |
17．如图是由若干个全等的等腰梯形拼成的四边形，四边形的周长与梯形的个数如表中所列，观察图形并思考当这个等腰梯形共有55个时，所拼成的图形的周长为（ ） 
| 梯形个数 | 1 | 2 | 3 | … |
| 图形周长 | 5a | 8a | 11a | … |
| A． | 167a | B． | 166a | C． | 165a | D． | 164a |
15．下列分式是最简分式的（ ）
| A． | $\frac{a+b}{{{a^2}+{b^2}}}$ | B． | $\frac{a}{{{a^2}-3a}}$ | C． | $\frac{2a}{{3{a^2}b}}$ | D． | $\frac{{{a^2}-ab}}{{{a^2}-{b^2}}}$ |