题目内容
18.在-3、-2、-1、0、1、2这六个数中,随机取出一个数记为a,那么使得关于x的一元二次方程x2-2ax+5=0无解,且使得关于x的方程$\frac{x+a}{x-1}$-3=$\frac{1}{1-x}$有整数解的所有a的值之和为( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 根据方程无解可得△<0即a2<5,解分式方程可得x=$\frac{a+4}{2}$,再6个数中找出满足a2<5且$\frac{a+4}{2}$为整数、$\frac{a+4}{2}$≠1的数即可得答案.
解答 解:∵一元二次方程x2-2ax+5=0无解,
∴△=(-2a)2-4×1×5=4a2-20<0,
即a2<5,
解方程$\frac{x+a}{x-1}$-3=$\frac{1}{1-x}$得:x=$\frac{a+4}{2}$,
∵在-3、-2、-1、0、1、2中使得a2<5且$\frac{a+4}{2}$为整数、$\frac{a+4}{2}$≠1的有0和2,
∴满足条件的所有a的值之和为2,
故选:D.
点评 本题主要考查一元二次方程根的判别式及解分式方程的能力,根据题意找到实数a需要满足的条件是解题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
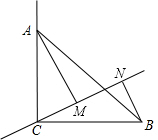 已知C点在直线MN上,∠ACB=90°,AC=BC,AM⊥MN,BN⊥MN,垂足分别是M、N.求证:MN=AM-BN.
已知C点在直线MN上,∠ACB=90°,AC=BC,AM⊥MN,BN⊥MN,垂足分别是M、N.求证:MN=AM-BN.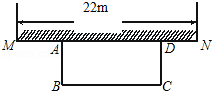 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用22m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用22m),现在已备足可以砌50m长的墙的材料. 如图,AB∥CD,∠A=98°,∠C=75°,∠B=105°,∠D=82°.
如图,AB∥CD,∠A=98°,∠C=75°,∠B=105°,∠D=82°.