题目内容
13.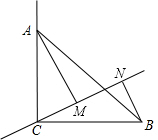 已知C点在直线MN上,∠ACB=90°,AC=BC,AM⊥MN,BN⊥MN,垂足分别是M、N.求证:MN=AM-BN.
已知C点在直线MN上,∠ACB=90°,AC=BC,AM⊥MN,BN⊥MN,垂足分别是M、N.求证:MN=AM-BN.
分析 利用同角的余角相等求出∠CAM=∠BCN,再利用“角角边”证明△ACM和△CBN全等,根据全等三角形对应边相等可得AM=CN,CM=BN,再根据MN=CN-CM等量代换即可得证.
解答 证明:∵AM⊥MN,
∴∠CAM+∠ACM=90°,
∵∠ACB=90°,
∴∠ACM+∠BCN=90°,
∴∠CAM=∠BCN,
∵AM⊥MN,BN⊥MN,
∴∠AMC=∠CNB=90°,
在△ACM和△CBN中,$\left\{\begin{array}{l}{∠CAM=∠BCN}\\{∠AMC=∠CNB=90°}\\{AC=BC}\end{array}\right.$,
∴△ACM≌△CBN(AAS),
∴AM=CN,CM=BN,
∵MN=CN-CM,
∴MN=AM-BN.
点评 本题考查了全等三角形的判定与性质,同角的余角相等的性质,熟练掌握三角形全等的判定方法并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
相关题目
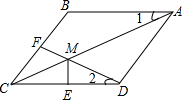 已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2. 如图,在△ABC中,AD平分∠BAC,若AB=10cm,AC=8cm,若S△ABD=15,那么S△ACD=12cm2.
如图,在△ABC中,AD平分∠BAC,若AB=10cm,AC=8cm,若S△ABD=15,那么S△ACD=12cm2.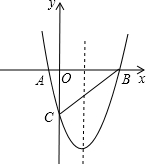 在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.