题目内容
10.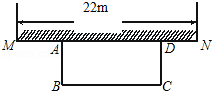 如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用22m),现在已备足可以砌50m长的墙的材料.
如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用22m),现在已备足可以砌50m长的墙的材料.(1)试设计一种砌法,使矩形花园的面积为300m2.
(2)这个矩形花园的面积能达到400m2吗?请说明理由.
分析 (1)根据可以砌50m长的墙的材料,即总长度是50米,设AB=x米,则BC=(50-2x)米,再根据矩形的面积公式列方程,解一元二次方程即可.
(2)同(1)联立方程,利用根的判别式判断即可.
解答 解:(1)设AB=x米,则BC=(50-2x)米.
根据题意可得,x(50-2x)=300,
解得:x1=10,x2=15,
当x=10,BC=50-10-10=30>22,
故x1=10(不合题意舍去),
当x=15时,BC=50-2×15=20(米).
答:可以围成AB的长为15米,BC为20米的矩形.
(2)花园的面积不能为400m2.
理由:由题意得x(50-2x)=400,
整理得:x2-25x+200=0,
∵△=625-4×200=-175<0,
∴此方程无解,
即花园的面积不能为400m2.
点评 本题考查了一元二次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系求解,注意围墙MN最长可利用22m,舍掉不符合题意的数据.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
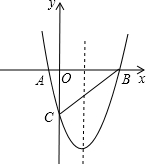 在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=x2-4x-5与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C. 如图,△ABC≌△A′B′C′,若BC′=9,B′C=2,则BB′的长度是3.5.
如图,△ABC≌△A′B′C′,若BC′=9,B′C=2,则BB′的长度是3.5. 如图是一个轴对称图形,解答下列问题:
如图是一个轴对称图形,解答下列问题: