题目内容
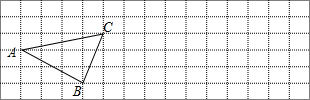
7. 小明到美丽的盐城滩涂参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.($\sqrt{3}$取1.73)
小明到美丽的盐城滩涂参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.($\sqrt{3}$取1.73)
分析 由已知作PC⊥AB于C,可得△ABP中∠A=60°∠B=45°且PA=100m,要求AB的长,可以先求出AC和BC的长.
解答  解:由题意可知:作PC⊥AB于C,
解:由题意可知:作PC⊥AB于C,
∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△ACP中,
∵∠ACP=90°,∠APC=30°,
∴AC=$\frac{1}{2}$AP=50,PC=$\sqrt{3}$AC=50$\sqrt{3}$.
在Rt△BPC中,
∵∠BCP=90°,∠BPC=45°,
∴BC=PC=50$\sqrt{3}$.
∴AB=AC+BC=50+50$\sqrt{3}$≈50+50×1.732≈136.6(米).
答:景点A与B之间的距离大约为136.6米
点评 本题考查了解直角三角形的应用,对于解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
19.若分式$\frac{{{x^2}-x-2}}{x+1}$的值为0,则x的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
17.下列说法正确的是( )
| A. | 单项式$\frac{2x{y}^{2}}{7}$的系数是2 | B. | 单项式$\frac{2x{y}^{2}}{7}$的次数是2 | ||
| C. | x2y-2x3y是四次多项式 | D. | x2y-2x3y有两项,分别是x2y和2x3y |
 已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF=7.5.
已知直线a∥b∥c,直线m,n与直线a,b,c分别交于点A,C,E,B,D,F,AC=4,CE=6,BD=3,则BF=7.5.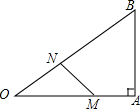 如图,在Rt△OAB中,∠A=90°,OA=4,AB=3,动点M从点A出发,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒$\frac{5}{4}$个单位长度的速度,沿OB向终点B移动.设运动时间为t秒.
如图,在Rt△OAB中,∠A=90°,OA=4,AB=3,动点M从点A出发,动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒$\frac{5}{4}$个单位长度的速度,沿OB向终点B移动.设运动时间为t秒. 如图,在△ABC中,AD是中线,G是重心,AD=6,则DG=2.
如图,在△ABC中,AD是中线,G是重心,AD=6,则DG=2.