题目内容
17.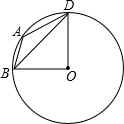 如图,⊙O是△ABD的外接圆,若∠A=135°,则∠BDO=90度.
如图,⊙O是△ABD的外接圆,若∠A=135°,则∠BDO=90度.
分析 本题要通过构造圆周角求解;在优弧AC上取一点E,连接AE、CE;由圆周角定理,易求得∠AEC的度数;再根据圆内接四边形的性质即可求出∠ABD的度数.
解答  解:在优弧BD上任意找一点E,连接BE、DE,
解:在优弧BD上任意找一点E,连接BE、DE,
根据圆内接四边形的性质,得∠E=45°,
根据圆周角定理,得∠BOD=2∠E=90°,
故答案为90.
点评 本题主要考查的是圆周角定理和圆内接四边形的性质.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
5.已知样本数据:3、2、4、3、x、4、5、7的极差是6,则样本数据的中位数是( )
| A. | 3 | B. | 4 | C. | 3.5 | D. | 3.5或4 |
12.数据分析:
射击教练为分析甲、乙两名运动员的射击成绩,随机统计了甲、乙各10次的射击成绩,整理得如下数据统计表:
(1)甲、乙射击成绩的众数各是多少?
(2)分别计算甲、乙的平均射击成绩;
(3)甲、乙两名运动员的射击成绩,谁的波动大?并说明理由.
射击教练为分析甲、乙两名运动员的射击成绩,随机统计了甲、乙各10次的射击成绩,整理得如下数据统计表:
| 射击成绩(环) | 6 | 7 | 8 | 9 | 10 |
| 甲射击频数 | 0 | 3 | 4 | 3 | 0 |
| 乙射击频数 | 1 | 3 | 2 | 3 | 1 |
(2)分别计算甲、乙的平均射击成绩;
(3)甲、乙两名运动员的射击成绩,谁的波动大?并说明理由.
6. 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,分别连接AD、BC,已知∠D=65°,则∠OCD=( )
如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,分别连接AD、BC,已知∠D=65°,则∠OCD=( )
 如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,分别连接AD、BC,已知∠D=65°,则∠OCD=( )
如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于E,分别连接AD、BC,已知∠D=65°,则∠OCD=( )| A. | 30° | B. | 35° | C. | 40° | D. | 45° |
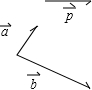 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{p}$,求作向量$\overrightarrow{p}$在$\overrightarrow{a}$、$\overrightarrow{b}$方向上的分向量.
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{p}$,求作向量$\overrightarrow{p}$在$\overrightarrow{a}$、$\overrightarrow{b}$方向上的分向量.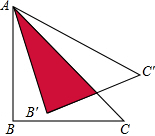 如图,直角△ABC的直角边AB的长为6cm,∠C=30°,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中两三角形重叠部分的面积等18 cm2.
如图,直角△ABC的直角边AB的长为6cm,∠C=30°,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中两三角形重叠部分的面积等18 cm2. 如图∠A=40°,∠ABD=∠D=∠F=90°,AG⊥GF于G,求∠E的度数.
如图∠A=40°,∠ABD=∠D=∠F=90°,AG⊥GF于G,求∠E的度数.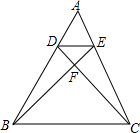 如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证:
如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证: