题目内容
8.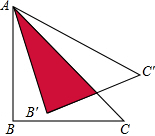 如图,直角△ABC的直角边AB的长为6cm,∠C=30°,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中两三角形重叠部分的面积等18 cm2.
如图,直角△ABC的直角边AB的长为6cm,∠C=30°,将△ABC绕点A逆时针旋转15°后得到△AB′C′,则图中两三角形重叠部分的面积等18 cm2.
分析 B′C′交AC于D,如图,利用互余得∠BAC=60°,再根据旋转的性质得AB′=AB=6,∠BAB′=15°,∠AB′C′=∠B=90°,则∠B′AD=45°,于是可判断△AB′D为等腰直角三角形,然后根据三角形的面积公式计算出S△AB′D即可.
解答 解:B′C′交AC于D,如图,
∵∠B=90°,∠C=30°,
∴∠BAC=60°,
∵△ABC绕点A逆时针旋转15°后得到△AB′C′,
∴AB′=AB=6,∠BAB′=15°,∠AB′C′=∠B=90°,
∴∠B′AD=60°-15°=45°,
∴△AB′D为等腰直角三角形,
∴B′D=AB′=6,
∴S△AB′D=$\frac{1}{2}$×6×6=18(cm2).
即图中两三角形重叠部分的面积等于18cm2.
故答案为18.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.在下列性质中,矩形具有而菱形不一定有的是( )
| A. | 对角线互相垂直 | B. | 对角线互相平分 | C. | 四个角是直角 | D. | 四条边相等 |
3. 如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )
如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )
 如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )
如图,是某校男子篮球队年龄分布条形统计图,这些年龄的众数和中位数分别为( )| A. | 14,15 | B. | 15,16 | C. | 15,15 | D. | 15,15.5 |
18.下列各式中,正确的是( )
| A. | -|-5|>0 | B. | -$\frac{4}{7}$>-$\frac{5}{7}$ | C. | |-0.4|<|+0.4| | D. | |-$\frac{1}{2}$|<0 |
 如图,已知线段AB与射线BC垂直,AB=2.把线段AB向右平移3个单位,那么AB扫过区域的面积是( )
如图,已知线段AB与射线BC垂直,AB=2.把线段AB向右平移3个单位,那么AB扫过区域的面积是( )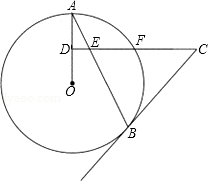 如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.
如图,AB是⊙O的弦,点D为OA上的一点,过点D作CD⊥OA于点D,交弦AB于点E,交⊙O于点F,且CE=CB.



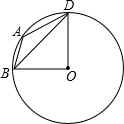 如图,⊙O是△ABD的外接圆,若∠A=135°,则∠BDO=90度.
如图,⊙O是△ABD的外接圆,若∠A=135°,则∠BDO=90度.