题目内容
14.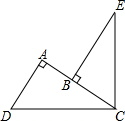 如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.
如图,∠DCE=90°,CD=CE,AD⊥AC,BE⊥AC,垂足分别为A、B,AD=3,AB=1.(1)求证:Rt△ACD≌△BEC;
(2)求BE的长.
分析 (1)由直角三角形的性质和同角的余角相等得出∠ACD=∠E,由AAS证明△ADC≌△BCE即可;
(2)由全等三角形的性质得出对应边相等AD=BC,BE=AC,即可得出结果.
解答 (1)证明:∵∠DCE=90°(已知),
∴∠ECB+∠ACD=90°,
∵EB⊥AC,
∴∠E+∠ECB=90°(直角三角形两锐角互余).
∴∠ACD=∠E(同角的余角相等).
∵AD⊥AC,BE⊥AC(已知),
∴∠A=∠EBC=90°(垂直的定义)
在Rt△ACD和Rt△BEC中,$\left\{\begin{array}{l}{∠A=∠EBC}&{\;}\\{∠ACD=∠E}&{\;}\\{CD=EC}&{\;}\end{array}\right.$,
∴Rt△ACD≌Rt△BEC(AAS).
(2)解:由(1)得:Rt△ACD≌Rt△BEC,
∴AD=BC,AC=BE(全等三角形的对应边相等),
∴AD+AB=BC+AB=AC.
∴BE=AD+AB=3+1=4.
点评 本题考查了三角形全等的判定及性质、直角三角形的性质;熟练掌握全等三角形的性质及判定,同一题中出现多个90°角的时候,往往通过互余求得角度相等,为三角形全等提供有用的条件,要掌握这种方法.

练习册系列答案
相关题目
 已知平面内有A,B,C三个点,按要求完成下列问题.
已知平面内有A,B,C三个点,按要求完成下列问题.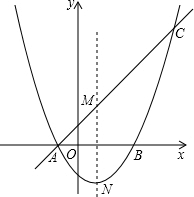 如图,抛物线y=$\frac{1}{2}$x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.
如图,抛物线y=$\frac{1}{2}$x2+mx+n交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.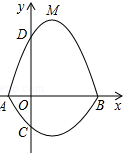 如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点.
如图,在平面直角坐标系xOy中,A、B为x轴上两点,C、D为y轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线成为“蛋线”.已知点C的坐标为(0,-$\frac{3}{2}$),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点. 如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.
如图,在△ABC中,AD是它的角平分线,且BD=CD,DE⊥AB于E,DF⊥AC于F.
 )数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
)数,如图,一层二叉树的结点总数为1,二层二叉树的点总数为3,三层二叉树的结点总数为7,…照此规律,你认为八层二叉树的结点总数为( )
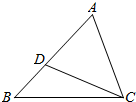 如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.
如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.