题目内容
12.我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树.(1)若我市2011年5万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?
(2)我市从2000年初开始实施天然林保护工程,大力倡导废纸回收再生,如今成效显著,森林面积大约由2009年初的1500万亩增加到2011年初的1815万亩.假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变,请你按全市总人口约为400万计算:在从2011年初到2012年初这一年度内,我市新增加的森林面积与回收废纸所能保护的最大森林面积之和最多可能达到多少亩.
分析 (1)根据每个初中毕业生离校时大约有10公斤废纸,用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树即可得出;
(2)利用增长率求法得出森林年均增长率,再得出天然保护增加数量以及废纸回收增加亩数,即可得出答案.
解答 解:(1)5×104×10÷1000×18÷80=112.5(亩).
因此若我市2011年5万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使112.5亩森林免遭砍伐;
(2)设我市森林面积年平均增长率为x,
依题意列方程得1500(1+x)2=1815,
解得x1=10%,x2=-2.1(不合题意,舍去),
所以2011年初到2012年初全市新增加的森林面积1815×104×10%=1815000(亩),
又因为全市因回收废纸所能保护的最大森林面积400×104×28×20%÷1000×18÷50=8064.
所以新增加的森林面积与回收废纸所能保护的最大森林面积之和最多可能达到的亩数:
1815000+8064=1823064(亩).
点评 此题主要考查了一元二次方程的应用,增长率问题是中考中考查重点,根据题意得出等式方程是解决问题的关键.

练习册系列答案
相关题目
2.某校九年级(1)、(2)班的全体学生进行跳绳体育测试,并从每班随机选取6名学生的测试成绩(单位:个)如下表:
(1)分别求九年级(1)、(2)两班随机选取6名学生的测试成绩的中位数;
(2)若只看九年级(1)、(2)两班随机选取的这6名学生,哪个班级的测试成绩更稳定?
(3)求九年级(1)、(2)班全体学生跳绳测试成绩的方差的估计值.
| 学生 | 1 | 2 | 3 | 4 | 5 | 6 |
| (1)班的成绩/个 | 77 | 81 | 74 | 84 | 78 | 80 |
| (2)班的成绩/个 | 79 | 77 | 80 | 77 | 79 | 82 |
(2)若只看九年级(1)、(2)两班随机选取的这6名学生,哪个班级的测试成绩更稳定?
(3)求九年级(1)、(2)班全体学生跳绳测试成绩的方差的估计值.
1.若原点是抛物线y=(m+1)x2的最高点,则m的取值范围是( )
| A. | m<0 | B. | m<1 | C. | m<-1 | D. | m>-1 |
 国家规定“中小学生每天在校体育活动时间不低于1h”,为此,某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
国家规定“中小学生每天在校体育活动时间不低于1h”,为此,某市就“每天在校体育活动”时间的问题随机调查了辖区内320名初中学生,根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是: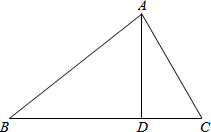 如图所示,在△ABC中,点D为BC边上的一点,AD=12,BD=16,AB=20,CD=9.
如图所示,在△ABC中,点D为BC边上的一点,AD=12,BD=16,AB=20,CD=9.