题目内容
2.已知关于x的方程$\frac{x+1}{x-1}-\frac{m}{{x}^{2}-1}=1$的解是正数,求m的取值范围.分析 分式方程去分母转化为整式方程,求出整式方程的解表示出x,根据解为正数,求出m的范围即可.
解答 解:去分母得:x2+2x+1-m=x2-1,
解得:x=$\frac{m-2}{2}$,
由分式方程的解为正数,得到$\frac{m-2}{2}$>0,且$\frac{m-2}{2}$≠1,
解得:m>2且m≠4.
点评 此题考查了分式方程的解,分式方程解为正数,即在分式方程有解的情况下x>0.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.下列说法中,错误的是( )
| A. | 两条对角线互相平分的四边形是平行四边形 | |
| B. | 两条对角线相等的四边形是矩形 | |
| C. | 两条对角线互相垂直的矩形形是正方形 | |
| D. | 两条对角线相等的菱形是正方形 |
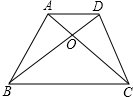 如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,若S△AOD=6,S△OBC=8,求梯形ABCD的面积.
如图,梯形ABCD中,AD∥BC,对角线AC、BD相交于O,若S△AOD=6,S△OBC=8,求梯形ABCD的面积.
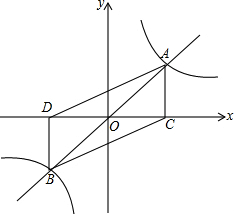 如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2.
如图,正比例函数y=$\frac{1}{2}x$与反比例函数y=$\frac{k}{x}(k>0)$的图象相交于A,B两点,过A点作AC⊥x轴,垂足为C,过B点作BD⊥x轴,垂足为D,已知点A的横坐标为2. 如图,△ABC在8×8的方格中位置如图所示,A(1,2),B(-2,0).
如图,△ABC在8×8的方格中位置如图所示,A(1,2),B(-2,0).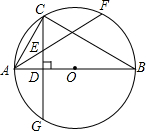 如图,⊙O是△ABC的外接圆,AB为直径,AC=CF,CD⊥AB于D,且交⊙O于G,AF交CD于E.求证:AE=CE.
如图,⊙O是△ABC的外接圆,AB为直径,AC=CF,CD⊥AB于D,且交⊙O于G,AF交CD于E.求证:AE=CE.