题目内容
2.某校九年级(1)、(2)班的全体学生进行跳绳体育测试,并从每班随机选取6名学生的测试成绩(单位:个)如下表:| 学生 | 1 | 2 | 3 | 4 | 5 | 6 |
| (1)班的成绩/个 | 77 | 81 | 74 | 84 | 78 | 80 |
| (2)班的成绩/个 | 79 | 77 | 80 | 77 | 79 | 82 |
(2)若只看九年级(1)、(2)两班随机选取的这6名学生,哪个班级的测试成绩更稳定?
(3)求九年级(1)、(2)班全体学生跳绳测试成绩的方差的估计值.
分析 (1)根据中位数的概念求出两班测试成绩的中位数;
(2)根据方差的计算公式:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],求出各自的方差,比较方差的大小进行判断即可;
(3)求出两班方差的平均数即可.
解答 解:(1)九年级(1)班随机选取6名学生的测试成绩的中位数为:$\frac{78+80}{2}$=79,
九年级(2)班随机选取6名学生的测试成绩的中位数为:$\frac{79+79}{2}$=79;
(2)九年级(1)班随机选取6名学生的测试成绩的平均数为:$\frac{1}{6}$(77+81+74+84+78+80)=79,
九年级(1)班随机选取6名学生的测试成绩的方差为:$\frac{1}{6}$[(77-79)2+(81-79)2+(74-79)2+(84-79)2+(78-79)2+(80-79)2]=10,
九年级(2)班随机选取6名学生的测试成绩的平均数为:$\frac{1}{6}$(79+77+80+77+79+82)=79,
九年级(2)班随机选取6名学生的测试成绩的方差为:$\frac{1}{6}$[(79-79)2+(77-79)2+(80-79)2+(77-79)2+(79-79)2+(82-79)2]=3,
∵3<10,
∴九年级(2)班的测试成绩更稳定;
(3)九年级(1)、(2)班全体学生跳绳测试成绩的方差的估计值=(10+3)÷2=6.5.
点评 本题考查的是方差的计算和中位数的确定,掌握方差的计算公式:S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立是解题的关键.

| A. | 第一、二、三象限 | B. | 第一、二、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
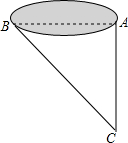 如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
如图所示,某工程队修建高速公路,需打通一条东西走向的隧道AB,为了测得AB的长,工程队在A处正南方向800米的C处测得BC=1000米,则隧道AB的长为600米.
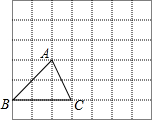 如图,已知三角形ABC,请根据下列提示作图:
如图,已知三角形ABC,请根据下列提示作图: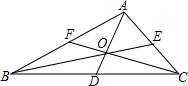 如图,已知△ABC的周长为36cm,BE,CF分别为边AC,AB上的中点,BE,CF相交于点O,AO的延长线交BC于点D,且AF=6cm,AE=4cm,求BD的长.
如图,已知△ABC的周长为36cm,BE,CF分别为边AC,AB上的中点,BE,CF相交于点O,AO的延长线交BC于点D,且AF=6cm,AE=4cm,求BD的长. 几何证明:
几何证明: