题目内容
9.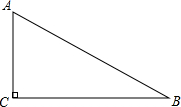 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.(1)用尺规在边BC上求作一点P.使PA=PB(不写作法,保留作图痕迹);
(2)连接AP,若AP平分∠CAB,AC=2,则BC=2$\sqrt{3}$.
分析 (1)直接利用线段垂直平分线的性质作出AB的垂直平分线进而得出答案;
(2)利用全等三角形的判定得出△ACP≌△ADP(AAS),进而得出AB的长,再利用勾股定理得出答案.
解答  解:(1)如图所示:P点即为所求;
解:(1)如图所示:P点即为所求;
(2)∵AP平分∠CAB,
∴∠CAP=∠PAD,
在△ACP和△ADP中
∵$\left\{\begin{array}{l}{∠C=∠ADP}\\{∠CAP=∠DAP}\\{AP=AP}\end{array}\right.$,
∴△ACP≌△ADP(AAS),
∴AC=AD,
∵AD=BD,
∴AB=4,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 此题主要考查了基本作图以及全等三角形的判定与性质等知识,得出△ACP≌△ADP是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列各组线段能构成直角三角形的一组是( )
| A. | 7,12,13 | B. | 30,40,50 | C. | 5,9,12 | D. | 3,4,6 |
 如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A、B两点,且点A的横坐标与点B的纵坐标都是-2.
如图,已知一次函数y=kx+b的图象与反比例函数y=-$\frac{8}{x}$的图象交于A、B两点,且点A的横坐标与点B的纵坐标都是-2.
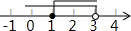
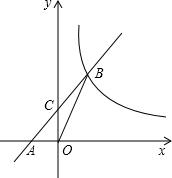 如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值.
如图,在平面直角坐标系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO,若S△OBC=1,tan∠BOC=$\frac{1}{3}$,求k2的值. 如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.
如图,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段,请在图中画出△ABC,使得AB=5,AC=$\sqrt{10}$,BC=$\sqrt{17}$,并求出此三角形的面积.