题目内容
11．
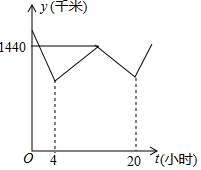甲、乙两车分别从A、B两地同时出发匀速相向而行，大楼C位于AB之间，甲与乙相遇在AC中点处，然后两车立即掉头，以原速原路返回，直到各自回到出发点．设甲、乙两车距大楼C的距离之和为y（千米），甲车离开A地的时间为t（小时），y与t的函数图象所示，则第21小时时，甲乙两车之间的距离为1350千米．
分析 设AC中点为E，根据乙车的运动速度不变结合函数图象，可得出AE=CE=2BC，进而可得出CE的长度，根据速度=路程÷时间即可求出甲、乙的运动速度，再根据两车之间的距离=两车速度和×掉头的时间，即可求出结论．
解答 解：设AC中点为E．
观察函数图象可知：乙车从B到C需用4小时，从C到E需用$\frac{20-4}{2}$=8小时，甲从A到E需要12小时，
∵点E为AC的中点，乙的速度不变，
∴AE=CE=2BC（如图所示）．
∵2CE=1440，
∴AE=720，BE=1080，
∴甲的速度为720÷12=60（千米/小时），乙的速度为1080÷12=90（千米/小时）．
第21小时时，甲乙两车之间的距离为（60+90）×（21-12）=1350（千米）．
故答案为：1350．
点评 本题考查一次函数的应用，据乙车的运动结合函数图象，找出AE=CE=2BC是解题的关键．
练习册系列答案
相关题目
1．某班在一次数学测验后成绩统计如下表：
如果60分及以上为及格，那么这次数学测验的及格率是90%．
| 分数段（分） | 40-49 | 50-59 | 60-69 | 70-79 | 80-89 | 90-100 |
| 人数 | 1 | 3 | 4 | 8 | 13 | 11 |
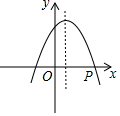如图，抛物线y=ax2+bx+c（a＜0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（3，0）在该抛物线上，则a-b+c的值为0．
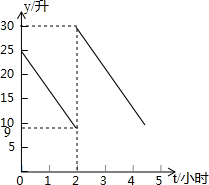张师傅驾车从甲地到乙地，两地相距500千米，汽车出发前油箱有油25升，途中加油若干升，加油前、后汽车都以100千米/小时的速度匀速行驶，已知油箱中剩余油量y（升）与行驶时间t（小时）之间的关系如图所示．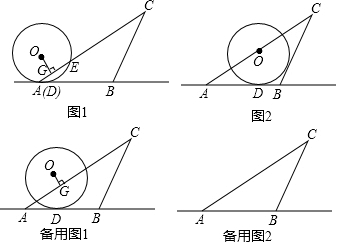
6．某服装店销售A、B两种品牌服装，且平均每月销售80件，已知这两种品牌服装的成本和售价如下表所示：
设该服装店每月销售的A品牌服装x件，平均每月获得的总利润为y元．
（1）写出y与x的函数关系式；
（2）如果该服装店平均每月投入的总成本不超过7500元，不考虑其他因素，那么当A、B两种品牌服装各销售多少件时，该服装店平均每月的总利润最大？并求出这个最大利润．
| A | B | |
| 成本（万元/件） | 100 | 80 |
| 售价（万元/件） | 170 | 120 |
（1）写出y与x的函数关系式；
（2）如果该服装店平均每月投入的总成本不超过7500元，不考虑其他因素，那么当A、B两种品牌服装各销售多少件时，该服装店平均每月的总利润最大？并求出这个最大利润．
小明和爸爸进行登山锻炼，两人同时从山脚下出发，沿相同路线匀速上山，小明用8分钟登上山顶，此时爸爸距出发地280米．小明登上山顶立即沿原路按某一速度匀速下山，与爸爸相遇后，和爸爸一起以原下山速度返回出发地．小明、爸爸在锻炼过程中离出发地的路程y1（米）、y2（米）与小明出发的时间x（分）的函数关系如图．