题目内容
19.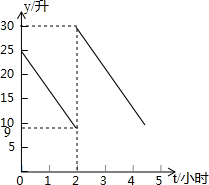 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.(1)写出加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式;
(2)途中加油多少升?
(3)汽车加油后还可行驶多少小时?
(4)汽车到达乙地时油箱中还余油多少升?
分析 (1)观察函数图象找出点的坐标,根据点的坐标利用待定系数法,即可求出加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式;
(2)根据途中加油量=加油后油箱中剩余油量-汽车停车加油时油箱中剩余油量,即可求出结论;
(3)根据还可行驶的时间=加油后油箱中剩余油量÷每小时耗油量,即可求出结论;
(4)根据时间=路程÷速度,可求出张师傅驾车从甲地到乙地路上所需时间,再根据汽车到达乙地时油箱中剩余油量=出发前油箱中剩余油量+途中加油量-每小时油耗×汽车行驶时间,即可求出结论.
解答 解:(1)设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b,
将(0,25)、(2,9)代入y=kt+b中,
$\left\{\begin{array}{l}{b=25}\\{2k+b=9}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-8}\\{b=25}\end{array}\right.$,
∴加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=-8t+25.
(2)30-9=21(升).
答:途中加油21升.
(3)30÷8=3.75(小时).
答:汽车加油后还可行驶3.75小时.
(4)500÷100=5(小时),
25+21-5×8=6(升).
答:汽车到达乙地时油箱中还余油6升.
点评 本题考查了一次函数的应用以及待定系数法求一次函数解析式,解题的关键是:(1)观察函数图象找出点的坐标,利用待定系数法求出y与t之间的函数关系式;(2)观察函数图象找出数据,列式计算;(3)根据数量关系,列式计算;(4)根据数量关系,列式计算.

练习册系列答案
相关题目
10.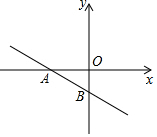 如图,一次函数y=ax+b的图象分别与x轴、y轴的负半轴相交于A、B,则下列结论一定正确的是( )
如图,一次函数y=ax+b的图象分别与x轴、y轴的负半轴相交于A、B,则下列结论一定正确的是( )
 如图,一次函数y=ax+b的图象分别与x轴、y轴的负半轴相交于A、B,则下列结论一定正确的是( )
如图,一次函数y=ax+b的图象分别与x轴、y轴的负半轴相交于A、B,则下列结论一定正确的是( )| A. | a-b>0 | B. | a+b>0 | C. | b-a>0 | D. | -a-b>0 |
8.将某抛物线图象向右平移2个单位,再向下平移3个单位所得的抛物线是y=-2x2+4x+1的图象,则将该抛物线沿y轴翻折后所得的函数关系式是( )
| A. | y=-2(x-1)2+6 | B. | y=-2(x-1)2-6 | C. | y=-2(x+1)2+6 | D. | y=2(x+1)2-6 |
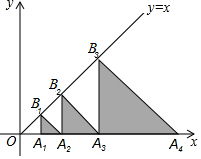 如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA1=1,则△B2016A2016A2017的面积为24029.
如图,△A1B1A2,△A2B2A3,△A3B3A4,…,△AnBnAn+1都是等腰直角三角形,其中点A1,A2,…,An在x轴上,点B1,B2,…,Bn在直线y=x上,已知OA1=1,则△B2016A2016A2017的面积为24029.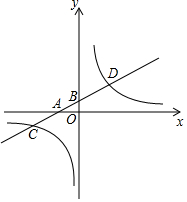 如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2.
如图,在平面直角坐标系中,一次函数y1=kx+b的图象分别交x轴,y轴于A、B两点,与反比例函数y2=$\frac{n}{x}$的图象交于C、D两点,已知点C的坐标为(-4,-1),点D的横坐标为2. 如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).
如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).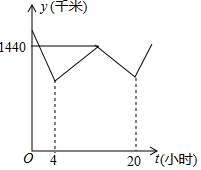 甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米.
甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为1350千米.