题目内容
12.计算:(1)$\sqrt{8}$+|$\sqrt{2}$-1|-π0+($\frac{1}{2}$)-1
(2)(-2$\sqrt{2}$)2÷($\sqrt{75}$+3$\sqrt{\frac{1}{3}}$-$\sqrt{48}$)
(3)先化简,后计算:$\frac{1}{a+b}$+$\frac{1}{b}$+$\frac{b}{a(a+b)}$,其中a=$\frac{\sqrt{5}+1}{2}$,b=$\frac{\sqrt{5}-1}{2}$.
分析 (1)根据零指数幂和负整数指数幂的意义计算;
(2)先把二次根式化为最简二次运算,然后把括号内合并后进行二次根式的除法运算;
(3)先通分,再化简,然后把x和y的值代入计算.
解答 解:(1)原式=2$\sqrt{2}$+$\sqrt{2}$-1-1+2
=3$\sqrt{2}$;
(2)原式=8÷(5$\sqrt{3}$+$\sqrt{3}$-4$\sqrt{3}$)
=8÷2$\sqrt{3}$
=$\frac{4\sqrt{3}}{3}$;
(3)原式=$\frac{ab+{a}^{2}+ab+{b}^{2}}{ab}$
=$\frac{(a+b)^{2}}{ab(a+b)}$
=$\frac{a+b}{ab}$,
当a=$\frac{\sqrt{5}+1}{2}$,b=$\frac{\sqrt{5}-1}{2}$时,a+b=$\sqrt{5}$,ab=1,
所以原式=$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.也考查了分式的化简求值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列语句:①$\sqrt{16}$的算术平方根是2;②$\sqrt{(-2)^{2}}$=±2;③-3是9的平方根;④$\root{3}{8}$=$\sqrt{4}$;⑤负数没有立方根,其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.在一个不透明的口袋里装有若干个质地相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,多次重复摸球.下表是多次活动汇总后统计的数据:
(1)请估计:当次数S很大时,摸到白球的频率将会接近0.3;假如你去摸一次,你摸到红球的概率是0.7(精确到0.1).
(2)试估算口袋中红球有多少只?
| 摸球的次数S | 150 | 200 | 500 | 900 | 1000 | 1200 |
| 摸到白球的频数n | 51 | 64 | 156 | 275 | 303 | 361 |
| 摸到白球的频率 | 0.34 | 0.32 | 0.312 | 0.306 | 0303 | 0.301 |
(2)试估算口袋中红球有多少只?
1.下列汽车标志中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

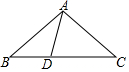 如图,在△ABC中,AB=AC=5,BC=8,点D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有3个.
如图,在△ABC中,AB=AC=5,BC=8,点D是线段BC上的动点(不含端点B,C),若线段AD的长为正整数,则点D的个数共有3个.