题目内容
5. 如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE
如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE(1)求证:BE=AD;
(2)若AC=6,AD=9,AE=3
①求证:△ABE是直角三角形;
②求△ACE的面积.
分析 (1)欲证明BE=AD,只要证明△BCE≌△ACD即可;
(2)①利用勾股定理的逆定理证明即可;
②作EH⊥AC于H.想办法求出EH即可解决问题;
解答 (1)证明:∵∠ACB=∠DCE=90°,AC=BC,CD=CE,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
$\left\{\begin{array}{l}{BC=CA}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD,
∴BE=AD.
(2)①证明:在Rt△ACB中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,
∵BE=AD=9,AE=3,
∴AB2+AE2=72+9=81,BE2=81,
∴AB2+AE2=BE2,
∴△ABE是直角三角形.
②解:作EH⊥AC于H.
∵∠BAE=90°,∠BAC=45°,
∴∠EAH=45°,
∴AH=HE,∵AE=3,
∴AH=HE=$\frac{3\sqrt{2}}{2}$,
∴S△ACE=$\frac{1}{2}$•AC•HE=$\frac{1}{2}$×6×$\frac{3\sqrt{2}}{2}$=$\frac{9\sqrt{2}}{2}$.
点评 本题考查全等三角形的判定和性质、勾股定理等逆定理、等腰直角三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造特殊三角形解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.在下列数:-3,0,1,-$\frac{1}{2}$中,属于负数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+$\frac{25\sqrt{3}}{2}$,其中正确的有( )
如图,D为等边三角形ABC内的一点,DA=5,DB=4,DC=3,将线段AD以点A为旋转中心逆时针旋转60°得到线段AD',下列结论:①点D与点D'的距离为5;②∠ADC=150°;③△ACD'可以由△ABD绕点A逆时针旋转60°得到;④点D到CD'的距离为3;⑤S四边形ABCD′=6+$\frac{25\sqrt{3}}{2}$,其中正确的有( ) 如图,在△ABC中,AB=5,AC=3,BC=4,D是BC边上一动点,BE⊥AD,交其延长线于点E,EF⊥AC,交其延长线于点F,则AF的最大值为4.
如图,在△ABC中,AB=5,AC=3,BC=4,D是BC边上一动点,BE⊥AD,交其延长线于点E,EF⊥AC,交其延长线于点F,则AF的最大值为4.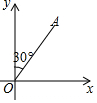 某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.
某港口在南北方向海岸线上的点O,甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,已知甲客轮沿着北偏东30°的方向航行.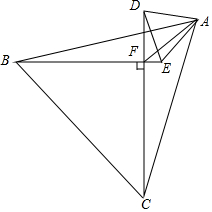 正△ABC,正△ADE,BE⊥CD,F为垂足,AF=1,求S△ABC+S△ADE.
正△ABC,正△ADE,BE⊥CD,F为垂足,AF=1,求S△ABC+S△ADE.