题目内容
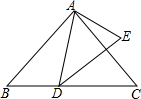如图，已知∠BAD=∠CAE，AB•AE=AD•AC．求证：∠C=∠E．考点：相似三角形的判定与性质
专题：证明题
分析：根据已知得出△ADE∽△ABC，进而得出∠BAC=∠DAE，即可得出答案．
解答：证明：∵AB•AE=AD•AC，
∴
=
，
∵∠BAD=∠CAE，
∴∠BAD+∠DAC=∠CAE+∠DAC，
∴∠BAC=∠DAE，
∴△ADE∽△ABC，
∴∠C=∠E．
∴
| AB |
| AD |
| AC |
| AE |
∵∠BAD=∠CAE，
∴∠BAD+∠DAC=∠CAE+∠DAC，
∴∠BAC=∠DAE，
∴△ADE∽△ABC，
∴∠C=∠E．
点评：此题主要考查了相似三角形的判定与性质，根据已知得出△ADE∽△ABC是解决问题的关键．
练习册系列答案
相关题目
已知△ABC中，∠A=2∠B=3∠C，则△ABC为（ ）
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、无法确定 |
如图，等腰梯形ABCD是一个四棱柱的俯视图，它的高为5，AD=3，AE⊥BC于点E，AE=4，BC=7，求此四棱柱的三种视图的面积和．
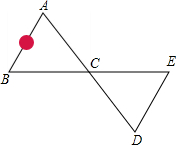如固，为修筑一条公路，需测量出被大石头阻挡的∠BAC的大小，为此，小张师傅便在直线AC上取点D，使AC=CD，在BC的延长线上取点E，使BC=CE，连接DE，只要测出∠D的度数，则可知∠A的度数等于∠D的度数．请说明理由．
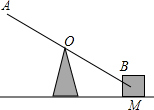如图，某人在A处利用杠杆抬起位于B处的重物M．已知重物M的质量为50kg，杠杆与地面的夹角为30°，在A处的人和B处的重物与支架的顶端O的水平距离都为3m．试问：该人将重物M抬至水平位置所做的功是多少焦耳（精确到0.1，
已知线段a，h（如图1、2），求作△ABC，使AB=AC=a，高AD=h．
如图，已知AB=CD，∠B=∠C，求证：△ABO≌△DCO．