题目内容
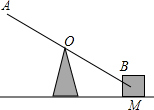 如图,某人在A处利用杠杆抬起位于B处的重物M.已知重物M的质量为50kg,杠杆与地面的夹角为30°,在A处的人和B处的重物与支架的顶端O的水平距离都为3m.试问:该人将重物M抬至水平位置所做的功是多少焦耳(精确到0.1,
如图,某人在A处利用杠杆抬起位于B处的重物M.已知重物M的质量为50kg,杠杆与地面的夹角为30°,在A处的人和B处的重物与支架的顶端O的水平距离都为3m.试问:该人将重物M抬至水平位置所做的功是多少焦耳(精确到0.1,| 3 |
考点:解直角三角形的应用-坡度坡角问题
专题:跨学科
分析:过B作O所在的水平线的垂线,垂足是D,求得BD的长,然后根据功的计算方法即可求解.
解答: 解:过B作O所在的水平线的垂线,垂足是D.
解:过B作O所在的水平线的垂线,垂足是D.
在直角△OBD中,BD=OD•tan30°=3×
=
≈1.73(米),
则该人将重物M抬至水平位置所做的功是:10×50×1.73=865(焦耳).
答:该人将重物M抬至水平位置所做的功是865焦耳.
 解:过B作O所在的水平线的垂线,垂足是D.
解:过B作O所在的水平线的垂线,垂足是D.在直角△OBD中,BD=OD•tan30°=3×
| ||
| 3 |
| 3 |
则该人将重物M抬至水平位置所做的功是:10×50×1.73=865(焦耳).
答:该人将重物M抬至水平位置所做的功是865焦耳.
点评:考查了解直角三角形的应用-坡度坡角问题,本题是跨学科问题,正确理解功的计算公式是关键.

练习册系列答案
相关题目
 如图,AB=AC,∠B=∠C,求证:△ABD≌△ACE.
如图,AB=AC,∠B=∠C,求证:△ABD≌△ACE.
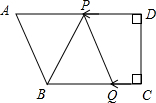 如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?
如图,在梯形ABCD中,AD∥BC,∠C=∠D=90°,BC=16,CD=12,AD=21.动点P从点D出发,沿线段DA的方向以每秒2个单位长度的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长度的速度向点B运动.点P,Q分别从点D,C同时出发,当点P运动到点A时,点Q随之停止运动.设运动时间为t(s),当t为何值时,以B,P,Q三点为顶点的三角形为等腰三角形?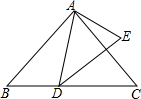 如图,已知∠BAD=∠CAE,AB•AE=AD•AC.求证:∠C=∠E.
如图,已知∠BAD=∠CAE,AB•AE=AD•AC.求证:∠C=∠E.
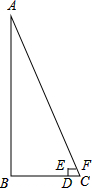 兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼第一级台阶上,并测得台阶上的影子长为0.2m,一级台阶高为0.3m,如图所示,其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地面上部分的长,ED的长为台阶高.若这棵树落在地面上的影长为4.4m,则树高为多少米?
兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1m的竹竿的影长为0.4m,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼第一级台阶上,并测得台阶上的影子长为0.2m,一级台阶高为0.3m,如图所示,其中AB为树高,EF为树影在第一级台阶上的影长,BD为树影在地面上部分的长,ED的长为台阶高.若这棵树落在地面上的影长为4.4m,则树高为多少米?