题目内容
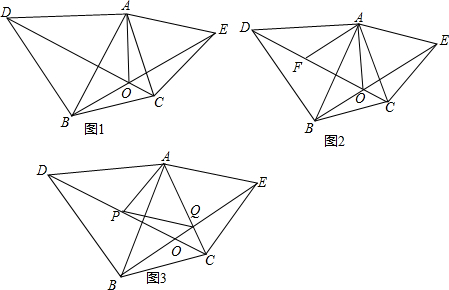
8.已知,如图,以△ABC的边AB、AC为边,分别在△ABC外作等边△ABD,等边△ACE.(1)如图1,求证:BE=CD;
(2)如图1,求∠BOC的度数;
(3)如图1,求证:AO平分∠DOE;
(4)如图2,求证:AO+BO=DO;
(5)如图3,若点P为CD的中点,点Q为BE的中点,求证:△APQ为等边三角形.
分析 (1)根据等边三角形性质得出AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,求出∠BAE=∠DAC.根据SAS证△ABE≌△ADC即可;
(2)根据全等求出∠ADC=∠ABE,在△DOB中根据三角形的内角和定理和∠ADB=∠DBA=60°即可求出答案;
(3)过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.根据三角形的面积公式求出AN=AM,根据角平分线性质求出即可;
(4)通过△DAC≌△BAE,得到∠1=∠2,于是得到∠4=∠DAB=60°,如图2,作等边三角形BOF,由于△BDF≌△BAO得到DF=AO,于是证得结论;
(5)由(4)证得△DAC≌△BAE,得到∠1=∠2,CD=BE,根据点P为CD的中点,点Q为BE的中点,于是得到PD=BQ,推出△ADP≌△ABQ,得到AP=AQ,∠3=∠4,根据等量代换即可得到结论.
解答  (1)证明:∵△ABD和△ACE都是等边三角形,
(1)证明:∵△ABD和△ACE都是等边三角形,
∴AB=AD,AE=AC,∠BAD=∠BDA=∠DBA=∠CAE=60°,
∴∠BAC+∠CAE=∠BAC+∠BAD,
即∠BAE=∠DAC.
在△ABE和△ADC中
∵$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAC}\\{AE=AC}\end{array}\right.$
∴△ABE≌△ADC(SAS),
∴BE=DC.
(2)解:由(1)知:△ABE≌△ADC,
∴∠ADC=∠ABE
∴∠ADC+∠BDO=∠ABE+∠BDO=∠BDA=60°
∴在△BOD中,∠BOD=180°-∠BDO-∠DBA-∠ABE
=180°-∠DBA-(∠ADC+∠BDO)
=180°-60°-60°
=60°.
(3)证明:如图1,过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.
∵由(1)知:△ABE≌△ADC,
∴S△ABE=S△ADC
∴-$\frac{1}{2}$BE•AM=$\frac{1}{2}$CD•AN,
∴AM=AN,
∴点A在∠DOE的平分线上,
即OA平分∠DOE;
(4)证明:∵∠DAC=60°+∠BAC,∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC与△BAE中,$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△DAC≌△BAE,
∴∠1=∠2,
∴∠4=∠DAB=60°,
如图2,作等边三角形BOF,
∵∠DBF=∠DBA-∠FBA=60°-∠FBA=∠2,
在△BDF与△BAO中,$\left\{\begin{array}{l}{BD=BA}\\{∠DBF=∠2}\\{BF=BO}\end{array}\right.$,
∴△BDF≌△BAO
∴DF=AO,
∴OD=OF+FD=OB+OA,
(5)证明: 由(4)证得△DAC≌△BAE,
由(4)证得△DAC≌△BAE,
∴∠1=∠2,CD=BE,
∵点P为CD的中点,点Q为BE的中点,
∴PD=BQ,
在△ADP与△ABQ中,$\left\{\begin{array}{l}{AD=AB}\\{∠1=∠2}\\{DP=BQ}\end{array}\right.$,
∴△ADP≌△ABQ,
∴AP=AQ,∠3=∠4,
∴∠3+∠PAB=60°,
∴∠PAB+∠4=60°,
∴△APQ为等边三角形.
点评 本题考查了等边三角形性质和判定,三角形的面积,全等三角形的性质和判定,三角形的内角和定理,正确的作出辅助线是解题的关键.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案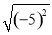 的结果是( )
的结果是( )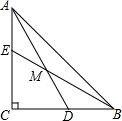 如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,
如图,△ABC中,AC=BC,∠ACB=90°,D,E分别是BC,AC上一点,BD=AE,BE,AD交于M,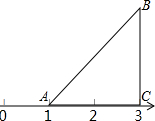 如图,等腰直角三角形ABC的直角边AC落在数轴上,点A表示的数是1,点C表示的数是3,以A为旋转中心逆时针旋转△ABC.
如图,等腰直角三角形ABC的直角边AC落在数轴上,点A表示的数是1,点C表示的数是3,以A为旋转中心逆时针旋转△ABC.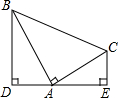 如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.
如图,Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,求DE的长.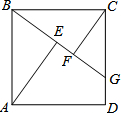 如图,在正方形ABCD中,点G是CD上任意一点,连接BG,作AE⊥BG于点E,CF⊥BG于点F.
如图,在正方形ABCD中,点G是CD上任意一点,连接BG,作AE⊥BG于点E,CF⊥BG于点F.