题目内容
13.解方程:(1)方程x2=2x的解为x1=0,x2=2;
(2)方程(x-2)2=1的解为x1=3,x2=1.
(3)方程(x-2)(x+5)=0的解为x1=2,x2=-5;
(4)方程x(x-1)=3(x-1)的解为x1=3,x2=1.
分析 (1)根据等式的性质,可化为一般式,根据因式分解,可得答案;
(2)根据等式的性质,可化为一般式,根据因式分解,可得答案;
(3)根据因式分解,可得答案;
(4)根据等式的性质,可化为一般式,根据因式分解,可得答案.
解答 解:(1)等号两边都减(2x),得
x2-2x=0.
因式分解,得
x(x-2)=0,
于是x=0或x-2=0,
解得x1=0,x2=2.
故答案为:x1=0,x2=2;
(2)等号两边都减1,得
(x-2)2-1=0,
因式分解,得
[(x-2)+1][(x-2)-1]=0,
于是x-1=0或x-3=0,
解得x1=3,x2=1,
故答案为:x1=3,x2=1;
(3)(x+5)(x-2)=0,
于是x+5=0或x-2=0,
解得x1=2,x2=-5,
故答案为:x1=2,x2=-5;
(4)等号两边都减3(x-1),得
x(x-1)-3(x-1)=0.
因式分解,得
(x-1)(x-3)=0,
于是x-3=0或x-1=0,
解得x1=3,x2=1.
故答案为:x1=3,x2=1.
点评 本题考查了解一元二次方程,利用因式分解法解一元二次方程的关键是分解因式.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
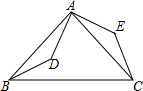 如图,点D是等腰直角三角形ABC内一点,AB=AC,将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌△ACE;若连结DE,AD=3,则DE=3$\sqrt{2}$.
如图,点D是等腰直角三角形ABC内一点,AB=AC,将△ABD绕点A逆时针旋转90°,点D与点E重合,则△ABD≌△ACE;若连结DE,AD=3,则DE=3$\sqrt{2}$.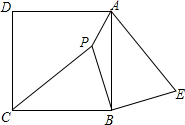 已知:如图,P是正方形ABCD内一点,△PCB顺时针旋转得到△ABE.
已知:如图,P是正方形ABCD内一点,△PCB顺时针旋转得到△ABE.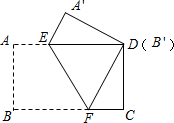 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积?
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=3cm,BC=5cm,则重叠部分△DEF的面积?