题目内容
某地要搭桥一座,桥的底部两端间的距离AB=l,称为跨度,桥面最高点到AB的距离为CD=h,当跨度和拱高确定时,有2种设计方案可供选择:①抛物线②圆弧形,已知这座桥跨度L=16m,拱高h=4m,求在距离桥的一端2m处欲立一桥墩支撑,在这两种方案中分别求桥墩的高度(由AB算起到桥拱为止).
考点:垂径定理的应用,二次函数的应用
专题:
分析:(1)根据题意画出图形,利用垂径定理以及勾股定理得出AO的长,再求出EF的长;
(2)根据交点式求出函数解析式,进而得出答案.
(2)根据交点式求出函数解析式,进而得出答案.
解答: 解:(1)如图所示:作EM⊥OC,可得EMDF为矩形.
解:(1)如图所示:作EM⊥OC,可得EMDF为矩形.
则EM=AD-AF=8-2=6,
∵OA2=OD2+AD2
∴OA2=82+(OA-4)2
∴OA=10(m),
∴OD=10-4=6(m),
∵OE2=EM2+OM2
∴OM=8m,
∴DM=2m,
∴EF=2m;
(2)以A为原点建立直角坐标系.
设解析式y=a(x-0)(x-16),
∵图象过C(8,4)点,
∴4=a(8-0)(8-16)
∴a=-
,
∴y=-
(x-0)(x-16),
当x=2,y=
,
∴EF=
.
 解:(1)如图所示:作EM⊥OC,可得EMDF为矩形.
解:(1)如图所示:作EM⊥OC,可得EMDF为矩形.则EM=AD-AF=8-2=6,
∵OA2=OD2+AD2
∴OA2=82+(OA-4)2
∴OA=10(m),
∴OD=10-4=6(m),
∵OE2=EM2+OM2
∴OM=8m,
∴DM=2m,
∴EF=2m;
(2)以A为原点建立直角坐标系.
设解析式y=a(x-0)(x-16),
∵图象过C(8,4)点,
∴4=a(8-0)(8-16)
∴a=-
| 1 |
| 16 |
∴y=-
| 1 |
| 16 |
当x=2,y=
| 7 |
| 4 |
∴EF=
| 7 |
| 4 |
点评:此题主要考查了垂径定理的应用以及二次函数的应用,根据题意画出图形结合勾股定理得出是解题关键.

练习册系列答案
相关题目
 下列图形①矩形;②菱形;③平行四边形;④正方形;⑤等腰三角形.能用如图两个全等的直角三角形拼成的是( )
下列图形①矩形;②菱形;③平行四边形;④正方形;⑤等腰三角形.能用如图两个全等的直角三角形拼成的是( )| A、①②③ | B、①②④ |
| C、③④⑤ | D、①③⑤ |
 已知:如图,在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,且D在边AB上,连结EC,取EC的中点M,连结DM和BM,将直角三角形ADE绕A点按逆时针旋转45°,结论:△BMD为等腰直角三角形,成立吗?
已知:如图,在Rt△ABC中,AB=BC,在Rt△ADE中,AD=DE,且D在边AB上,连结EC,取EC的中点M,连结DM和BM,将直角三角形ADE绕A点按逆时针旋转45°,结论:△BMD为等腰直角三角形,成立吗?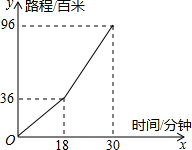 “懒洋洋”由于身体太胖,决定每天早上起来锻炼身体,帮助减肥,已知“懒洋洋”从“羊村”出发到森林里,先上坡后下坡,行程状况如图所示;若返回时上坡和下坡的速度扔保持不变,那么“懒洋洋”从森林到“羊村”所用的时间是
“懒洋洋”由于身体太胖,决定每天早上起来锻炼身体,帮助减肥,已知“懒洋洋”从“羊村”出发到森林里,先上坡后下坡,行程状况如图所示;若返回时上坡和下坡的速度扔保持不变,那么“懒洋洋”从森林到“羊村”所用的时间是