题目内容
19.下列二次根式中是最简二次根式的是( )| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{15}$ | D. | $\frac{3}{\sqrt{2}}$ |
分析 结合最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.进行解答即可.
解答 解:A、$\sqrt{24}$=2$\sqrt{6}$,故$\sqrt{24}$不是最简二次根式,本选项错误;
B、$\sqrt{\frac{1}{3}}$=$\frac{\sqrt{3}}{3}$,故$\sqrt{\frac{1}{3}}$不是最简二次根式,本选项错误;
C、$\sqrt{15}$是最简二次根式,本选项正确;
D、$\frac{3}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,故$\frac{3}{\sqrt{2}}$不是最简二次根式,本选项错误.
故选C.
点评 本题考查了最简二次根式,解答本题的关键在于熟练掌握最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.

练习册系列答案
相关题目
7.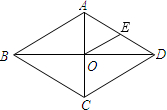 如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点E是AD边的中点,连接DE,则OE的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点E是AD边的中点,连接DE,则OE的长为( )
 如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点E是AD边的中点,连接DE,则OE的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,AC=6,BD=8,点E是AD边的中点,连接DE,则OE的长为( )| A. | 10 | B. | $\frac{5}{2}$ | C. | 5 | D. | 4 |
4. 如图,函数y=3x和y=kx+3的图象相交于点A(m,2),则不等式3x<kx+3的解集为( )
如图,函数y=3x和y=kx+3的图象相交于点A(m,2),则不等式3x<kx+3的解集为( )
 如图,函数y=3x和y=kx+3的图象相交于点A(m,2),则不等式3x<kx+3的解集为( )
如图,函数y=3x和y=kx+3的图象相交于点A(m,2),则不等式3x<kx+3的解集为( )| A. | x$<\frac{2}{3}$ | B. | x$>\frac{2}{3}$ | C. | x$<\frac{3}{2}$ | D. | x$>\frac{3}{2}$ |
11. 如图,已知AB∥CD,CF平分∠AFE,∠C=36°,则∠FED的度数是( )
如图,已知AB∥CD,CF平分∠AFE,∠C=36°,则∠FED的度数是( )
 如图,已知AB∥CD,CF平分∠AFE,∠C=36°,则∠FED的度数是( )
如图,已知AB∥CD,CF平分∠AFE,∠C=36°,则∠FED的度数是( )| A. | 28° | B. | 56° | C. | 62° | D. | 72° |
 已知:如图所示,正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M,求证:△ABF≌△DAE.
已知:如图所示,正方形ABCD中,E、F分别是边CD、DA上的点,且CE=DF,AE与BF交于点M,求证:△ABF≌△DAE. 若用半径为9,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是( )
若用半径为9,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是( ) 已知有理数a,b,c在数轴上的位置如图所示,化简|c-a|-|a+b|+|b-c|.
已知有理数a,b,c在数轴上的位置如图所示,化简|c-a|-|a+b|+|b-c|.