题目内容
19．
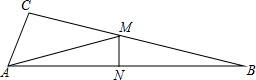如图，已知在Rt△ABC中，∠C=90°，∠B=15°，AB的垂直平分线分别与AB、BC相交于点N、M，联结AM，AC=6，求BM的长．
分析 根据线段垂直平分线得出AM=BM，求出∠B=∠MAB=15°，求出∠AMC=30°，根据含30度角的直角三角形性质求出AM=2AC=BM．
解答 解∵M在AB的垂直平分线上，
∴AM=BM，
∴∠B=∠MAB=15°，
∴∠AMC=15°+15°=30°，
∵∠C=90°，
∴BM=AM=2AC=12．
点评 本题考查了勾股定理，含30度角的直角三角形，三角形的外角性质，线段垂直平分线性质等知识点，关键是运用定理求出BM=AM=2AC．
练习册系列答案
相关题目
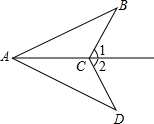如图，已知△ABC≌△ADC，∠1=64°，则∠2的度数是64°．
用反证法证明命题“已知D，E分别为△ABC的边AB，AC上的点，BE，CD交于点F，则BE，CD不能互相平分”是真命题．
如图，AB⊥BC，DC⊥BC，AE⊥CD，∠DAE=30°，∠DBC=45°，AB=2，求CD．
如图，⊙0的半径为5cm，点O到直线1的距离OD=3cm，l与⊙O相交于A、B两点，则线段AB上到点O的距离为整数的点有5个．