题目内容
4.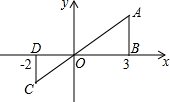 如图,△AOB的三个顶点的坐标分别是A(3,2)、O(0,0)、B(3,0),若△COD与△AOB是位似图形,且位似比为2:3,则点C的坐标为(-2,-$\frac{4}{3}$),点D的坐标为(-2,0).
如图,△AOB的三个顶点的坐标分别是A(3,2)、O(0,0)、B(3,0),若△COD与△AOB是位似图形,且位似比为2:3,则点C的坐标为(-2,-$\frac{4}{3}$),点D的坐标为(-2,0).
分析 利用位似图形的性质得出对应点坐标的关系:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.进而得出答案.
解答 解:∵△COD与△AOB是位似图形,且位似比为2:3,A(3,2),
∴点C的坐标为:(-2,-$\frac{4}{3}$),点D的坐标为:(-2,0).
故答案为:(-2,-$\frac{4}{3}$),(-2,0).
点评 此题主要考查了位似变换,根据题意得出对应点坐标的关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19. 如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
 如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
16.已知x1=5,x2=-5是一元二次方程x2+ax+b=0的两个根,则a,b的值为( )
| A. | a=25,b=-25 | B. | a=0,b=-25 | C. | a=25,b=25 | D. | a=0,b=25 |
14.下列各组数的大小比较错误的是( )
| A. | -$\frac{2}{3}$>-$\frac{3}{4}$ | B. | -$\frac{1}{3}$<-0.3 | C. | -(-2)>+(-3) | D. | -(-2.5)<|-2$\frac{1}{4}$| |
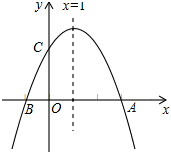 如图:二次函数y=ax2+bx+c的图象与x轴交A、B两点,与y轴交于C点,且对称轴为x=1,点B的坐标是(-1,0),则下面四个结论:①2a+b=0,②4a-2b+c<0,③ac<0,④当y<0时,x<-1或x>3,其中正确的个数是( )
如图:二次函数y=ax2+bx+c的图象与x轴交A、B两点,与y轴交于C点,且对称轴为x=1,点B的坐标是(-1,0),则下面四个结论:①2a+b=0,②4a-2b+c<0,③ac<0,④当y<0时,x<-1或x>3,其中正确的个数是( )