题目内容
19. 如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
分析 根据相似多边形的对应边成比例列出方程,解方程即可得到答案.
解答 解:设矩形的长是a,宽是b,
∵剩下的矩形与原矩形相似,
∴$\frac{a}{b}$=$\frac{b}{a-b}$,
整理得:a2-ab-b2=0,
两边同除以b2,得($\frac{a}{b}$)2-$\frac{a}{b}$-1=0,
解得$\frac{a}{b}$=$\frac{\sqrt{5}+1}{2}$或$\frac{-\sqrt{5}+1}{2}$(舍去).
∴长与宽的比为:$\frac{\sqrt{5}+1}{2}$.
故选:D.
点评 本题考查的是相似多边形的性质,根据相似多边形的性质列出方程,解方程是解决本题的关键.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | a2+a=a3 | B. | (a3)2=a5 | C. | $\sqrt{3}$×$\sqrt{3}$=3 | D. | $\sqrt{16}$-$\sqrt{9}$=$\sqrt{7}$ |
 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.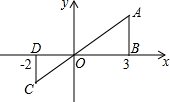 如图,△AOB的三个顶点的坐标分别是A(3,2)、O(0,0)、B(3,0),若△COD与△AOB是位似图形,且位似比为2:3,则点C的坐标为(-2,-$\frac{4}{3}$),点D的坐标为(-2,0).
如图,△AOB的三个顶点的坐标分别是A(3,2)、O(0,0)、B(3,0),若△COD与△AOB是位似图形,且位似比为2:3,则点C的坐标为(-2,-$\frac{4}{3}$),点D的坐标为(-2,0).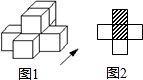 如果用□表示一个立方体,用阴影■表示三个立方体叠加,那么如图1所示由7个立方体叠成的几何体,小明同学从上方观察,画出的平面图形如图2所示.请画出从正前方和左面观察到的平面图形.
如果用□表示一个立方体,用阴影■表示三个立方体叠加,那么如图1所示由7个立方体叠成的几何体,小明同学从上方观察,画出的平面图形如图2所示.请画出从正前方和左面观察到的平面图形.