题目内容
12.在平面直角坐标系中,A(2,0),B(0,3),若△ABC的面积为6,且点C在坐标轴上,则符合条件的点C的坐标为(0,9)或(0,-3)或(-2,0)或(6,0)..分析 点C在y轴上,利用三角形的面积求出BC的长,再分点C在点B的上方与下方两种情况求出OC,然后写出点C的坐标即可;点C在x轴上时,利用三角形的面积求出AC,再分点C在点A的左边与右边两种情况求出OC,然后写出点C的坐标.
解答 解:当点C在y轴上,A(2,0),
∴S△ABC=$\frac{1}{2}$BC•2=6,
解得BC=6,
若点C在点B的上方,则OC=3+6=9,
所以,点C(0,9),
若点C在点B的下方,则OC=3-6=-3,
所以,点C(0,-3),
若点C在x轴上,∵点C在x轴上,B(0,3),
∴S△ABC=$\frac{1}{2}$AC•3=6,
解得AC=4,
若点C在点A的左边,则OC=2-4=-2,
所以,点C(-2,0),
若点C在点A的右边,则OC=4+2=6,
所以,点C(6,0),
综上所述,点C的坐标为(0,9)或(0,-3)或(-2,0)或(6,0).
故答案为:(0,9)或(0,-3)或(-2,0)或(6,0).
点评 本题考查了坐标与图形性质,三角形的面积,难点在于分情况讨论,坐标轴要分x轴与y轴两种情况.

练习册系列答案
相关题目
17.已知点$({-1,{y_1}}),({-3\frac{1}{2},{y_2}}),({\frac{1}{2},{y_3}})$都在抛物线y=3(x+1)2-2上,则y1,y2,y3的大小关系为( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y2>y3>y1 | D. | y3>y1>y2 |
1.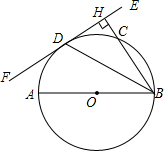 如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.
如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.
(1)求证:EF是⊙O的切线;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
 如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.
如图,AB为⊙O的直径,D是⊙O上一点,过D点作直线EF,BH⊥EF交⊙O于点C,垂足为H,且BD平分∠ABH.(1)求证:EF是⊙O的切线;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
2.用计算器计算时,其按键顺序为: ,则其运算结果为( )
,则其运算结果为( )
 ,则其运算结果为( )
,则其运算结果为( )| A. | -8 | B. | -6 | C. | 6 | D. | 8 |
 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.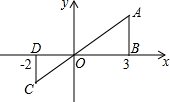 如图,△AOB的三个顶点的坐标分别是A(3,2)、O(0,0)、B(3,0),若△COD与△AOB是位似图形,且位似比为2:3,则点C的坐标为(-2,-$\frac{4}{3}$),点D的坐标为(-2,0).
如图,△AOB的三个顶点的坐标分别是A(3,2)、O(0,0)、B(3,0),若△COD与△AOB是位似图形,且位似比为2:3,则点C的坐标为(-2,-$\frac{4}{3}$),点D的坐标为(-2,0).