题目内容
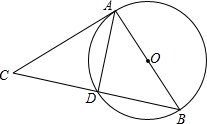如图，AC切圆O于A，CB顺次交圆O于D、B点，AC=6，DB=5，连接AD、AB．证明：△CAD∽△CBA．考点：切线的性质,相似三角形的判定
专题：证明题
分析：根据有两组角对应相等的两个三角形相似可得到△CAD∽△CBA．
解答：证明：∵AB是直径，
∴∠ADB=90°．
又∵CA是切线，
∴BA⊥AC，
∴∠BAC=90°．
∴∠BAC=∠CDA=90°．
又∵∠BCA=∠DCA，
∴△CAD∽△CBA．
∴∠ADB=90°．
又∵CA是切线，
∴BA⊥AC，
∴∠BAC=90°．
∴∠BAC=∠CDA=90°．
又∵∠BCA=∠DCA，
∴△CAD∽△CBA．
点评：此题主要考查相似三角形的判定及切线的性质的理解及运用．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．
练习册系列答案
名校课堂系列答案
相关题目
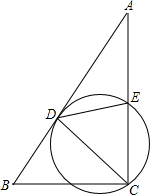如图，在△ABC中，∠ACB=90°，∠A=30°，经过点C的⊙O与直线AB相切于点D，与AC交于E，⊙O的半径为1，当CD平分∠ACB时，求CE的长是多少．
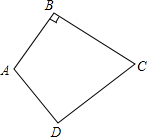如图，有一张四边形纸片ABCD，AB=AD=6cm，CB=CD=8cm，且∠B=90°．
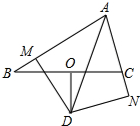如图，△ABC中，O是BC的中点，D是∠BAC平分线上一点，且DO⊥BC，过点D分别作DM⊥AB于M，DN⊥AC于N．求证：
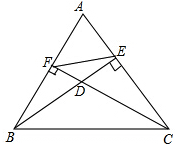如图，BE、CF分别是△ABC的边AC、AB上的高，BE与CF相交于点D，求证：