题目内容
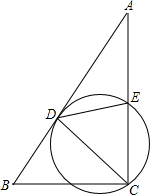 如图,在△ABC中,∠ACB=90°,∠A=30°,经过点C的⊙O与直线AB相切于点D,与AC交于E,⊙O的半径为1,当CD平分∠ACB时,求CE的长是多少.
如图,在△ABC中,∠ACB=90°,∠A=30°,经过点C的⊙O与直线AB相切于点D,与AC交于E,⊙O的半径为1,当CD平分∠ACB时,求CE的长是多少.考点:切线的性质
专题:
分析:首先连接OD,OC,作OH⊥CE于H,进而得出∠ODC=15°,即可得出∠HCO=30°,再利用锐角三角函数关系求出答案.
解答: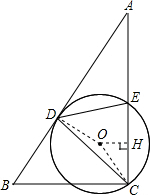 解:如图所示:
解:如图所示:
连接OD,OC,作OH⊥CE于H,
∵∠ACB=90°,CD平分∠ACB,
∴∠BCD=∠ECD=45°,
又∵∠A=30°,
∴∠B=60°,
∴∠ADC=105°,
∵经过点C的圆O与直线AB相切于点D,
∴OD⊥AB,
∴∠ODA=90°,
∴∠ODC=15°,
∵OD=OC,
∴∠OCD=∠ODC=15°,
∴∠HCO=30°,
∵OC=1,OH⊥HC,
∴CH=COcos30°=
,
∴CE=2CH=
.
 解:如图所示:
解:如图所示:连接OD,OC,作OH⊥CE于H,
∵∠ACB=90°,CD平分∠ACB,
∴∠BCD=∠ECD=45°,
又∵∠A=30°,
∴∠B=60°,
∴∠ADC=105°,
∵经过点C的圆O与直线AB相切于点D,
∴OD⊥AB,
∴∠ODA=90°,
∴∠ODC=15°,
∵OD=OC,
∴∠OCD=∠ODC=15°,
∴∠HCO=30°,
∵OC=1,OH⊥HC,
∴CH=COcos30°=
| ||
| 2 |
∴CE=2CH=
| 3 |
点评:此题主要考查了切线的性质以及垂径定理和角平分线的定义等知识,得出∠HCO=30°是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
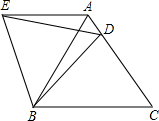 在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是
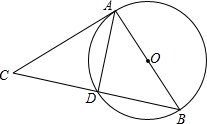 如图,AC切圆O于A,CB顺次交圆O于D、B点,AC=6,DB=5,连接AD、AB.证明:△CAD∽△CBA.
如图,AC切圆O于A,CB顺次交圆O于D、B点,AC=6,DB=5,连接AD、AB.证明:△CAD∽△CBA.